English
新興国・途上国のいまを知る
アジア経済研究所>IDEスクエア>コラム>途上国研究の最先端>第84回　先生それPハクです──なぜ実証研究の結果はいつも「効果あり」なのか?《途上国研究の最先端》（伊藤 成朗）

IDEスクエア

コラム

途上国研究の最先端

第84回　先生それPハクです──なぜ実証研究の結果はいつも「効果あり」なのか?

#URPHacking, sensei: Why are all the empirical results “statistically significant”? (We should botch these words)

PDF版ダウンロードページ：https://hdl.handle.net/2344/0002001059

2024年7月

（4,003字）

今回紹介する研究

Abel Brodeur, Scott Carrell, David Figlio, and Lester Lusher. 2023. “Unpacking p-hacking and publication bias.” American Economic Review 113 (11): 2974–3002.

なぜか分からないけど、効果があってほしい

データを使った実証研究では統計学的な仮説検定をします。たとえば、最低賃金を引き上げると失業が増えるという仮説の検定は、

失業率 = a + b * 最低賃金 + 誤差

という式で係数bが正か検定します。具体的には、統計プログラムなどでbを推計して推計値 b ^ を得ます。推計値 b ^ が正だったとしても、誤差で正になっている可能性もあるので、誤差を考慮しても正か、つまり、真の値bが統計学的にゼロと違うと判断できるか検定します1。なお、以下では本文は日常用語表現に努め、より正確な表現は脚注に記すことにします。

この統計学的推論では、 b = 0 が正しいと想定し、得た推計値 b ^ が（ b = 0 からすると）どれだけ極端かを問います。真の値が b = 0 の場合に推計値 b ^ 以上の値を観察する確率が分かれば、得た推計値 b ^ がどれだけ極端かの判断材料になります。この「 b = 0 が正しいときに、得た推計値 b ^ 以上の値を観察する確率」をp値といいます2。p値が小さければ、

p値が小さい
⇒
b = 0 が正しいと想定すると極端なことが起こっている
⇒
b = 0 が正しいと想定するのは誤りなのでは
⇒
真の値bは統計学的にゼロではない

と判断します。

このように、実証研究では、p値が小さいと「効果ありという発見」といえます3。逆に、p値が大きいと「効果なしという発見」といえます4。読者の皆さんは、「効果ありという発見」と「効果なしという発見」のどちらに興味をそそられるでしょうか。

筆者にとっては「効果ありという発見」の方が目を引きます。え、そうなの、という反応になることが多いのに対し、「効果なしという発見」は、あ、そう、で終わりがちです。予想どおりの結果であったとしても、効果ありの場合は、やっぱりそうか、なのに対し、効果なしの場合は、そんなの当たり前でしょ、になりがちです。なぜそうなるのか分かりませんが、多くの人が筆者と同じ反応をすると思っています。

実は研究者の多くも同じです。今日紹介する論文でミクロ経済学研究者に実施した匿名調査では、p値が小さくないと学術雑誌に掲載されないのでは、と思っている人の割合は8割を超えているのです5。

効果がないので効果を出そう──pハッキング

学術雑誌などがp値の小さい研究を選んで掲載することを出版バイアス（publication bias）といいます。出版バイアスを予期している、効果ありの方が良い、など様々な動機から、研究者がp値を小さくする作業をpハッキング（または分岐道、forking paths）といいます。

多くのpハッキングは研究者が意図したものです。推計方法をいじくり回して、p値が小さくなるように仕向ける。幾つか推計をして、p値が小さい結果だけを報告する。効果が出るまで実験を繰り返す。

一方、意図せずpハッキングになってしまうこともあります。推計結果が出てから結果に合うように仮説を選ぶのは、p値が小さいことが先に決まっているので検定とはいえず、pハッキングです（Hypothesize After Results are Known, HARKingともいいます）。ほかにも、推計をしてp値が大きいために、モティベーションを失って論文を書かないことも意図しないpハッキングです。なぜならば、p値の大きい研究をお蔵入りさせ、p値の小さい研究だけを世に出しているので、結局はp値を小さくする作業になるからです。

pハッキングは誤解を広める

pハッキングが横行すると、効果ありという（p値が小さい）研究ばかり世に出て、効果なしという研究は日の目を見ません。すると、効果ありなんだ、という誤解が世に広まります。しかも、誤解であることに誰も気づきません。だから、pハッキングは困った行為なのです。

pハッキングをもたらすこれらの行為は、疑わしい研究行為（questionable research practices, QRPs）の一部です。文科省などは、研究倫理に照らしてやってはいけない、と指導しています。QRPをする研究者は研究者同士の信頼を失い、研究予算を得にくくなります。しかし、作業過程を隠せばバレないですし、不公正な行為という意識が乏しいことも手伝い、経済学論文でpハッキングは横行している……か検討したのが今回紹介するブロデューたちの研究です。

データ

データは、2013～2018年にJournal of Human Resources（JHR）誌に投稿された全3607論文、各査読段階の判定結果、各論文に割り当てられた編者と査読者の情報です。論文からは、主たる結果のp値を抜き出します。さらに、著者たちの見解を調べるために、投稿者全員561名に匿名調査を依頼し、143名（25.49％）から回答を得ています。

pハッキングと出版バイアスを検定する方法

多数の論文からp値を抜き出し、ヒストグラムを描いたとします。その頂点を結んだ線をpカーブといいます6、7。図1の青いpカーブのように、急に増える右上がりの凸部分があるとpハッキングが示唆されます。

図1　pカーブ

図1　pカーブ

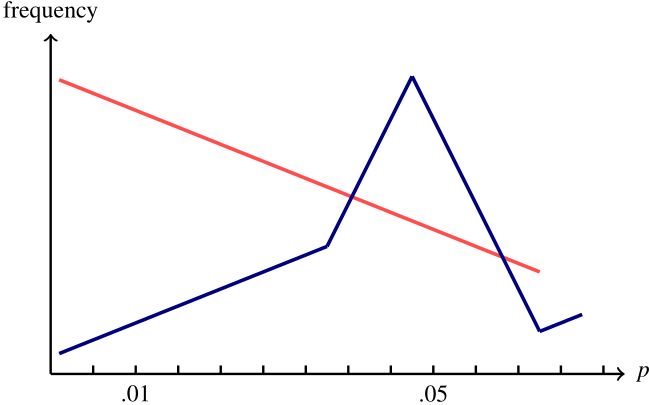
（注）赤いpカーブは効果が大きくpハッキングがない場合、
青いpカーブは効果が小さくpハッキングがある場合。
（出所）筆者作成

図2　帰無仮説の分布、効果大の分布、効果小の分布、pハックされた効果小の分布

図2　帰無仮説の分布、効果大の分布、効果小の分布、pハックされた効果小の分布

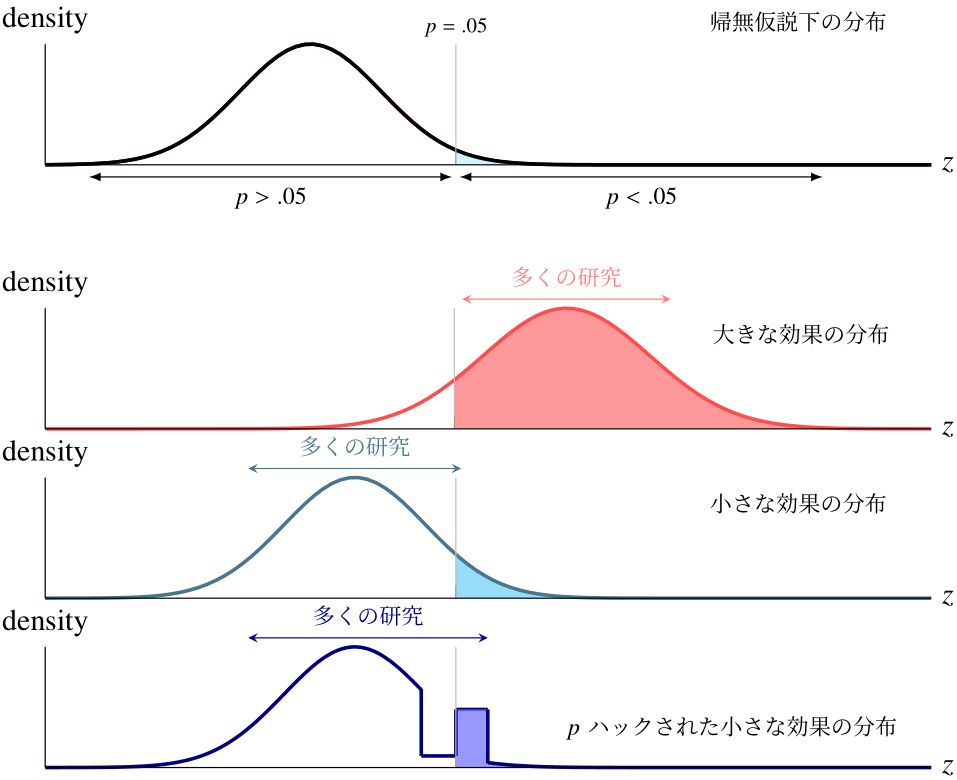
（注）研究数の分布。図を見やすくするために、p=.10やp=.01を
目指したpハッキングは捨象して描いている。
（出所）筆者作成

真に効果ありの場合、推計値は0よりも大きい場合が多いので、図2の赤い分布のようにp値の小さな研究が多数あります。真の効果が十分に大きい場合、誰もpハッキングしなければ、図1でp値が有意水準として参照される.05近傍よりも、.01近傍の研究が多くなります。つまり、図1の赤い線のようにpカーブは右下がりになります。

真に効果がない場合には、図2の淡い青い分布のようにp値の小さな研究は少ししかありません。ここでpハッキングがあると、p値を有意水準として参照される.05以下よりも小さくする（図2で自分の推計結果を右に移動させる）作業を研究者がするので、図2の濃い青色の分布のように、研究数は.05以上部分で減り、.05未満部分で増えます。つまり、図1で0から右に進んでいくときに、.05直前で増えるためにその周辺で右上がりになります。「有意水準」として参照される.05や.01よりも小さい値周辺で、pカーブが右上がりかを検定すれば、pハッキング有無の検定になるのです。

経済学で同様の計測研究は他にもありますが、本論文の強みは、とある学術雑誌の初稿（雑誌が投稿を受領した段階での原稿）から最終稿（雑誌が掲載した段階での原稿）の詳細情報を入手することで、投稿者側が仕組んだpハッキングと雑誌側が仕向けた出版バイアスの影響を別々に計測した点です。つまり、初稿は投稿者たちの行動の影響だけが反映されているのに対し、最終稿には投稿者たちの行動＋雑誌側の方針が反映されているはずです。よって、初稿と最終稿を比較すれば、雑誌による出版バイアスの影響をある程度計測できるのです8。

図3　初稿のp値の分布

図3　初稿のp値の分布

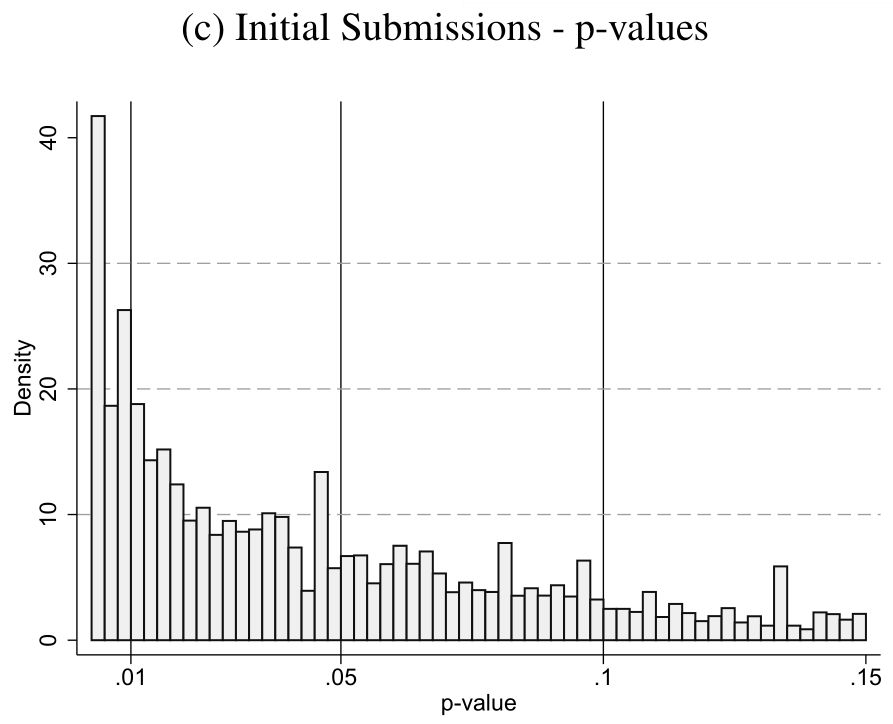
（出所）Brodeur, Carrell, Figlio and Lusher (2023), Figure 2

pハッキングは蔓延している

結果は一目瞭然です。pカーブで右上がりの部分が.01、.05、.1で見て取れます9。先行研究でも同じ傾向で、経済学全体にpハッキングが蔓延していることが分かります。著者たちの匿名調査では、トップ・ジャーナルに論文を掲載した一流の研究者の20％～40％が過去5年に各種QRPに手を染めた、とも回答しており、問題の深刻さが分かります10。

一方、初稿と最終稿の比較では、pハッキングの程度は両者で変わらないことが分かりました。つまり、この雑誌で出版バイアスは確認できません。出版バイアスは小さそうですが、この雑誌はpハッキングのある論文もない論文も同じ程度に掲載しています。よって、この雑誌はpハッキングを追認しているともいえそうです。pハッキングを見破るには投稿者以外による推計再現作業が必要なので、雑誌側の体制が整わず追認するしかないのかもしれません。

なぜpハックするのか

JHR誌のように出版バイアスがない雑誌でも、研究者たちがあると思い込めば、pハックするでしょう11。著者たちは、研究者がpハックしないように、分析前計画（pre analysis plan）を公開して、データを扱う前にどのような推計をするか決めてしまう制度などを推奨しています。

確かに予防効果はあると思いますが、データを見る前に分析方法を決められない場合もあります12。こうした場合には、幾つかの雑誌が共同歩調を取って査読過程を公開するなど、出版バイアスがあるという誤解を解くことも有効だと思います。JHR誌の場合、実在しない心配から研究者がpハッキングに手を染めるという、ばかげた状況を回避できます。また、すべての論文で推計再現作業をすると宣言すれば、pハッキングがバレると恐れた研究者がpハックしなくなるか、推計再現作業をしない雑誌に投稿先を変えるかもしれません。

そもそも、最低賃金が失業を増やす「効果あり」か「効果なし」か、研究者にとってどちらでも良いはずです。それなのに、とくに利益もないのに「効果あり」にしようと血道を上げるのは愚かです。標本サイズが大きければ、小さな効果も検知できます。ですから、標本サイズを大きくすることに努め、小さな効果でも「効果あり」と判定できる、だけど効果は小さいから無視可能、と論じられるような研究をすべきなのでしょう。しかし、そうすると大規模なデータや実験が必要で、若手研究者は困ってしまいます。予算のない研究者は、小規模な分析でも注目される斬新なアイディアか、ほどほどの標本サイズでも検知できる効果の大きい現象を見つけるしかないのでしょうか。アイディアかお金か、どちらかがないと悩ましいことになりそうです。

※この記事の内容および意見は執筆者個人に属し、日本貿易振興機構あるいはアジア経済研究所の公式意見を示すものではありません。
参考文献
著者プロフィール

伊藤成朗（いとうせいろう）　アジア経済研究所 開発研究センター、ミクロ経済分析グループ長。博士（経済学）。専門は開発経済学、応用ミクロ経済学、応用時系列分析。最近の著作に「南アフリカにおける最低賃金規制と農業生産」（『アジア経済』 2021年6月号）、主な著作に“The effect of sex work regulation on health and well-being of sex workers: Evidence from Senegal.” （Aurélia Lépine, Carole Treibichと共著、Health Economics, 2018, 27(11): 1627-1652）など。

書籍：南アフリカにおける最低賃金規制と農業生産

書籍：The effect of sex work regulation on health and well-being of sex workers: Evidence from Senegal

注
  1. 推計値 b ^ 、観察数（標本サイズ）をもとに、 b = 0 という帰無仮説が棄却されるかt検定（片側検定）します。
  2. 正確に言うと、「帰無仮説 b = 0 が正しいときに、得た推計値 b ^ 以上の値を観察する確率」がP値です。P値とは帰無仮説が成立する確率、と説明されることもありますが、正確ではありません。P値は帰無仮説 H 0 が正しいときに手元にあるデータDよりも極端なデータを観察する確率 1 － P ( D | H 0 ） です。よって、手元のデータを得たときに帰無仮説が正しい（成立する）確率 P ( H 0 | D ） ではありません。
  3. 正確には、「効果がないこと（＝帰無仮説）を強く疑問視する発見」です。疑問視するとは、帰無仮説下で起こりづらいことが起きた、という意味です。
  4. 正確には、「効果がないこと（＝帰無仮説）を強く疑問視しない発見」です。疑問視しないとは、帰無仮説下で起こりやすいことが起きた、という意味です。
  5. 正確には、編者の意思決定に統計的有意が重要な要因だ、と回答しています。
  6. 専門用語を使うと、pカーブとは各論文から集めたp値の確率密度関数で、 P < 0.15 程度の範囲のものを指します。
  7. 帰無仮説 b = 0 が正しい場合、pカーブは水平になります。推計値以上の値を観察する確率がp値ですが、ここでp値が.05だとしましょう。仮に、推計値が少し小さくなったとき、推計値以上の値を観察する確率は5％から6％になるとします。つまり、p値が1％ポイント増えるということは、推計値以上の値を観察する確率は1％増えます。p値が.1であれ.2であれ（＝pカーブのどの点であれ）、p値が1％増えるときには、推計値以上の値を観察する確率は常に1％増えています。つまり、ヒストグラムを描くと、p値がどの水準でも、同じだけの頻度（高さ）を伴います。言い換えると、pカーブはどの点でも常に同じ高さなので、水平です。
  8. 雑誌が直面する原稿と雑誌が選んで改訂をした原稿の対比です。初稿の一部しか最終稿にならないので、編集と選抜の両方の過程を経ています。
  9. 粗い四捨五入で.05が増える影響も考えねばなりません（Kranz and Putz 2022）。たとえば、推計値が0.015、標準誤差が0.014の場合、そのままz値を計算すると0.015/0.014=1.07ですが、四捨五入して計算すると0.02/0.01=2.00になります。こうした研究を取り除いてpハッキング検定をする必要があるといわれていますが、このような粗い四捨五入をすること自体にpハッキングの意図があるとも思えます。よって、粗い四捨五入の研究も含めた図を見るべきだと思います。
  10. pカーブの傾きが右上がりということだけでは、pハッキングの浸透度は分かりません。このため、著者たちは研究者たちに匿名調査を実施して、どのくらいの割合でQRPがあるのか計測しています。
  11. 出版バイアス以外のpハックする動機としては、経済理論の裏付けに乏しい仮説を扱っていることも考えられます。「風が吹けば桶屋が儲かる」のように、理論的裏付けの乏しい（疑わしい）仮説は、データで支持されると意外だからこそ注目されます。儲かる「効果なし」だと誰からも注目されず、雑誌で出版することは難しいでしょう。再現性が乏しく、今や原著者ですら存在を疑問視した心理学のプライミング仮説も、「効果あり」だったからこそ注目を集めました。検討に値しない仮説を扱うと、無理して「効果あり」を演出する誘因が出てきます。
  12. 2次データを使った観察研究では、情報がどの程度豊富か分からないので、事前に決められる内容に限りがあります。
【特集目次】

途上国研究の最先端