IDEスクエア
コラム
第55回 マクロ・ショックの測り方――バーティクのインスピレーションの完成形
Fomalising Bartik’s insights: Impact evaluation of macro shocks
PDF版ダウンロードページ：http://hdl.handle.net/2344/00052920
2022年2月
（3,662字）
今回紹介する研究
Kirill Borusyak, Peter Hull, Xavier Jaravel: “Quasi-experimental shift-share research designs,” Review of Economic Studies, Vol.89, Issue 1, January 2022, pp.181-213.
マクロ・ショック分析は開発ミクロ経済学の王道
干ばつになると一般に農村の所得は減少する。しかし、細かく見ていくと、影響の度合いは村によって違う。工場のある村では所得に対する影響がより小さい。さらに細かく見ると、同じ村でも農家によって所得への影響が違う。灌漑農地を持つ農家は天水農地に依存する農家よりも、干ばつの影響が軽微だ。
開発経済学では、干ばつがもたらす家計レベルの影響を、共通のショック（降雨量の減少率など）と各家計の曝露度（天水農地の比率など）を掛け合わせた変数の影響として捉え、所得減少が子どもの就学に与える効果などを推計してきた。ショックが大きいほど、またショックへの曝露度が高いほど、所得を通じて就学などへの影響が強くなることを許容した推計である1。天候、価格、政策など、途上国の家計や企業に影響を与えるマクロ・ショックは多い。開発ミクロ経済学と銘打っていても、広範囲に及ぶマクロ・ショックの影響を推計する研究は多い。すべての主体を含む因果関係（平均治療効果）を推計できるのは、実験を除けば自然実験と呼ばれるマクロ・ショックしかない、と主張する研究者もいる（Rosenzweig and Wolpin 2000）。
バーティク操作変数の光と影
ショックとシェア（ショックへの曝露度）の積を使うこの手法は、経済地理分野でティモシー・バーティク（Timothy J. Bartik）が1991年に初めて使ったとされる。バーティクは都市における非農業雇用の拡大が賃金に与える影響を推計するとき、労働需要の拡大によって雇用が増える場合のみを取り上げる工夫をした。というのも、労働需要の拡大によって雇用が増えるときは賃金が上がり、労働供給の拡大によって雇用が増えるときは賃金が減るので、労働需要と労働供給が同時に動いて雇用が拡大すると、賃金に与える効果は定まらないからである。
労働需要によって雇用が増える場合は、非農業財・サービスへの需要が増えて生産が拡大しているケースを取り上げればよい。バーティクは各都市の非農業需要は政策や価格など国単位のマクロ・ショックに影響されると仮定し、国全体の非農業生産の成長というショックと各都市の雇用における非農業シェアとの積を使っている。それ以降、シェアとショックの積はバーティク操作変数（Bartik instruments）と呼ばれている。
バーティク操作変数はすぐに計算できるので便利だが、使う立場の分析者は常に不安と隣り合わせにあった。というのも、シェアが因果関係を見誤らせる欠落変数（omitted variables）を取り込んでいる可能性を捨てきれないからだ。計量経済学の言葉で表現すると、バーティク操作変数はシェアを通じて妥当性（validity)が疑われる。
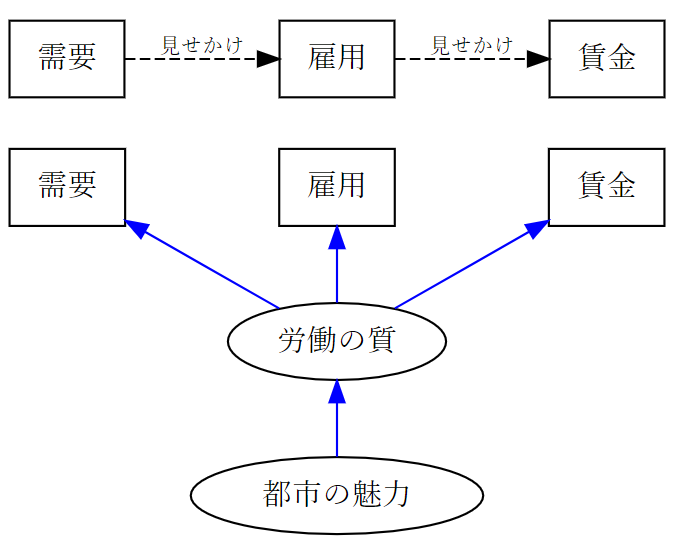
干ばつの例を考えよう。天水農地の比率が高いほど干ばつで子どもの就学率が下がる傾向にあったとしても、天水農地を耕作する比率が高い家計とは、もともと能力が低くて教育投資の収益率が低い家計かもしれない。すると、干ばつを契機に低下した就学率は、天水農地の比率とは関係なく、教育投資への魅力の弱さによってそもそも低下する傾向にあったかもしれない（図1）。非農業需要⇒雇用によって賃金が増えたと推計された都市は、そもそも都市の魅力が強いために優秀な人材を引き寄せ、優秀な人材を求めて非農業部門が雇用シェアを高め、優秀な人材だからこそ賃金が伸びたのかもしれない。仮にこれが事実とすれば、シェアは人材の優秀さという労働供給要因を捉えていることになる。そして、都市の魅力が強いほど、非農業雇用の拡大幅と賃金増加幅も大きい。つまり、都市の魅力⇒質の高い労働⇒非農業雇用シェア⇒賃金、という因果関係がある。ここで雇用や賃金の伸びは、全国非農業生産成長というマクロ・ショックがなくても起こっていることに留意したい。このとき、非農業需要を捉えるという想定のバーティク操作変数（＝シェア×全国非農業成長）は、計算式にシェアを含むため、シェアの値が高い都市ほど「需要」の伸びを高く算出する。ここで、シェアが大きく「需要」の伸びが高い都市は、供給側要因によって優秀な人材が多く賃金もより上昇している都市でもある。すると、「需要」の伸びが高い都市ほど賃金上昇が大きいことになり、需要⇒雇用⇒賃金という実際には存在しない因果関係を示すように見える（図2）。つまり、需要の計算式に使うシェアが供給側要因を反映している場合には、供給と需要を混同し、需要起因の因果関係として推計してしまう2。
これらの例では、シェアは観察できない能力や魅力（欠落変数）を反映しており、一方で欠落変数は結果の差も生んでいる。であれば、結果とバーティク操作変数（シェア×ショック）は欠落変数に応じて変化しているだけであり、シェア×ショックが結果に影響しない場合でも、あたかもシェア×ショック⇒結果という因果関係のように推計されてしまうかもしれない。
図1 所得と就学率の因果関係
（上段は見せかけの関係、下段は真の関係、楕円は欠落変数）
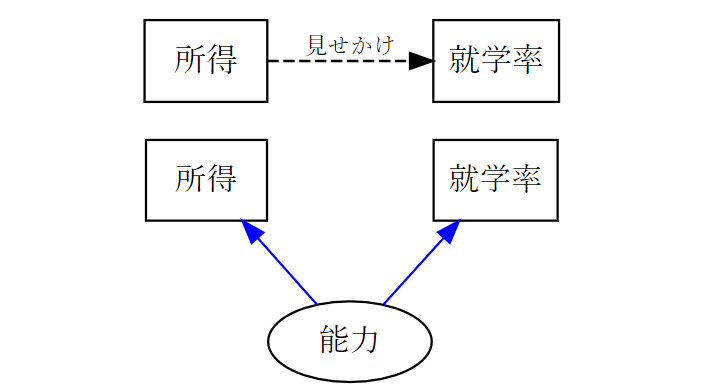
図2 需要と賃金の因果関係
（上段は見せかけの関係、下段は真の関係、楕円は欠落変数）
ショックがランダムで期間が長ければOK
上記2例は開発経済学と経済地理のクラシックな実証方法だが、シェア×ショックという変数を用いて因果関係を推計できるのか、これまで計量経済学的（＝統計学的）な裏付けはなかった。むしろ、推計した結果は、シェア起因の因果関係と混同している可能性が懸念されていた。
ボルシャク・ハル・ジャラヴェルは、バーティク操作変数から結果への因果関係が正しく得られる条件を解明した。ここまでショックが一種類のケースを考えてきたが、著者たちは一般的なケースとして、さまざまなショックとその曝露度の加重平均で影響を考えている。例えば、中国製品の輸入がもたらす影響を考える場合、さまざまな産業について中国製品の輸入がどれだけ増加したかというショックを、それぞれの地域の産業シェアで加重平均したものが、各地域のシェア×ショックとなる3。
著者たちによると、ショックがランダムで、ショックの種類が多く、ショックが多くの主体（地域）に影響していれば、シェアと結果は欠落変数に影響されてもよい。さらに、複数期間収集されるパネル・データでは、ショックが1つ（ショックの種類が僅か）でも期間数が長ければ、もしくは、期間数が短くても主体（地域）数とショックの種類が多ければ、因果関係を正しく得られる。とくに、パネル・データに関する結果は胸を撫で下ろす朗報である4。このため、ショックがランダムと考えられるのかに注意し、ショックの種類が少なくてもパネル化して期間数を増やすことを目指せば、もしくは、期間数が短くても主体数とショックの種類を多く見出せば、分析者は信頼性のある因果関係を推計できる。バーティクの優れたインスピレーションは、ここに計量経済学としても完成形になったといえる。
ただし、限界もある。著者らの推計方法はショック種類数と期間を観察単位にする。このために、精度の高い推計には、少なくともショックの種類か期間のいずれかが多く観察されなければならない。たとえば、主体数が1000、ショックが1種類、期間が2期だと、推計に使うデータの標本サイズはショック種類数×期間＝2でしかなく、意味のある推計はできない。下記のナンとキアンの研究も、著者らの方法を使うと実質的な標本サイズは35（期間)でしかない。このため、著者らの方法は、バーティク操作変数による推計値が妥当か確認することから使われ始めるかもしれない。
さまざまな応用例
バーティク操作変数は人気があり、応用例が多い。米国の食料援助が受け入れ国で争乱を引き起こすことを示したナンとキアンの研究も、バーティク操作変数を使っている。米国の食料生産がショックで、食料援助受け入れ率がシェアである（Nunn and Qian 2014）。鉱物資源価格の急騰が採掘場のある国の騒乱を増やすことを示したバーマンらの研究もバーティク操作変数を使う。鉱物価格がショックで、面積当たり鉱物採掘場の存在率がシェアである（Berman et al. 2017）。目新しく映る例として、賃金のジェンダー格差が女性へのドメスティク・バイオレンスに与える影響も、アイザがバーティク操作変数を使って推計している。ショックは女性従業員比率が高い（女性の賃金を高めやすい）産業の国全体での成長、各地のシェアはこうした産業の被雇用者が全被雇用者数に占める割合である（Aizer 2010）。ショックがランダムで各主体のショック曝露度が異なる現象は途上国にもたくさんある。開発経済学でもバーティク操作変数を使った研究が増えることが予想される。
参考文献
- Aizer, Anna. 2010. “The Gender Wage Gap and Domestic Violence.” American Economic Review, 100 (4): 1847–59.
- Autor, David H., David Dorn, and Gordon H. Hanson. 2013. “The China Syndrome: Local Labor Market Effects of Import Competition in the United States.” American Economic Review, 103 (6): 2121–68.
- Berman, Nicolas, Mathieu Couttenier, Dominic Rohner, and Mathias Thoenig. 2017. “This Mine Is Mine! How Minerals Fuel Conflicts in Africa.” American Economic Review, 107 (6): 1564–1610.
- Goldsmith-Pinkham, Paul, Isaac Sorkin, and Henry Swift. 2020. “Bartik Instruments: What, When, Why, and How.” American Economic Review, 110 (8): 2586–2624.
- Nunn, Nathan, and Nancy Qian. 2014. “US Food Aid and Civil Conflict.” American Economic Review, 104 (6): 1630–66.
- Rosenzweig, Mark, and Kenneth I. Wolpin. 2000. “Natural ‘Natural Experiments’ in Economics.” Journal of Economic Literature, 38 (4): 827–74.
著者プロフィール
伊藤成朗（いとうせいろう） アジア経済研究所 開発研究センター、ミクロ経済分析グループ長。博士（経済学）。専門は開発経済学、応用ミクロ経済学、応用時系列分析。最近の著作に”The effect of sex work regulation on health and well-being of sex workers: Evidence from Senegal.” （Aurélia Lépine, Carole Treibichと共著、Health Economics, 2018, 27(11): 1627-1652）、主な著作に「南アフリカにおける最低賃金規制と農業生産」（『アジア経済』 2021年6月号）など。
注
- 正確には、所得という内生変数に対処するためにシェアとショックの積を操作変数として使っている。また、本コラムでも頻出する二重差分（DID）推計値は、ショック曝露に「あり、なし」という二項変数を使ったバーティク操作変数推計と見なすこともできる。ショックの有無という粗い情報よりも、ショックの程度というきめ細かな情報を使うため、バーティク操作変数推計値は影響の多様さを示すことができる。
- 計量経済学の言葉で表現すると、バーティク操作変数と誤差項が供給要因という共通の変数を持つ（＝妥当性validityを満たさない）ために、推計値は過大推計される。
- Autor, Dorn, and Hanson（2013）は、全米各地における中国からの輸入の影響をバーティク操作変数で推計している。
- ショックの種類が多いケースは部門別関税引き上げなど、限定された応用例以外、開発経済学では見つかりそうにない。よって、期間数の長さで因果関係を見出せるという結果は特に朗報である。なお、Goldsmith-Pinkham, Sorkin, and Swift（2020）は、ショックではなくシェアがランダムな場合において、バーティク操作変数で因果関係を得られることを示している。
- 第1回 途上国ではなぜ加齢に伴う賃金上昇が小さいのか？
- 第2回 男児選好はインドの子供たちの発育阻害を説明できるか
- 第3回 子供支援で希望を育む
- 第4回 後退する民主主義
- 第5回 しつけは誰が？――自然実験としての王国建設とその帰結
- 第6回 途上国の労働市場で紹介が頻繁に利用されるのはなぜか
- 第7回 絶対的貧困線を真面目に測り直す――1日1.9ドルではない
- 第8回 労働移動の障壁がなくなれば一国の生産性はどの程度向上するのか
- 第9回 科学の世界の「えこひいき」――社会的紐帯とエリート研究者の選出
- 第10回 妻の財産権の保障がHIV感染率を引き下げるのか
- 第11回 飲酒による早期児童発達障害と格差の継続――やってはいけない実験を探す
- 第12回 長期志向の起源は農業にあり
- 第13回 その選択、最適ですか？――通勤・通学路とロンドン地下鉄ストライキが示す習慣の合理性
- 第14回 貧困者向け雇用政策を問い直す
- 第15回 妻（夫）がどれだけお金を使っているか、ついでに二人の「愛」も測ります
- 第16回 先読みして行動していますか？――米連邦議会上院議員の投票行動とその戦略性
- 第17回 保険加入率を高めるための発想の転換
- 第18回 いつ、どこで「国家」は生まれるか？――コンゴ戦争と定住武装集団による「建国」
- 第19回 婚資の慣習は女子教育を引き上げるか
- 第20回 産まれる前からの格差――胎内ショックの影響
- 第21回 貧困層が貯蓄を増やすには？――社会的紐帯と評判
- 第22回 農業技術普及のキーパーソンは「普通の人」
- 第23回 勤務地の希望を叶えて公務員のやる気を引き出す
- 第24回 信頼できる国はどこですか？
- 第25回 なぜ経済抗議運動に参加するのか――2010年代アフリカ諸国の分析
- 第26回 景気と経済成長が出生率に与える影響
- 第27回 消費者すべてが税務調査官だったら――ブラジル、サンパウロ州の脱税防止策
- 第28回 最低賃金引き上げの影響（その１） アメリカでは雇用が減らないらしい
- 第29回 禁酒にコミットしますか？
- 第30回 通信の高速化が雇用創出を促す―― アフリカ大陸への海底ケーブル敷設の事例
- 第31回 最低賃金引き上げの影響（その2）ハンガリーでは労働費用増の4分の3を消費者が負担したらしい
- 第32回 友達だけに「こっそり」やさしくしますか？ 国際制度の本質
- 第33回 モラルに訴える――インドネシア、延滞債権回収実験とその効果
- 第34回 「コネ」による官僚の人事決定とその働きぶりへの影響――大英帝国、植民地総督に学ぶ
- 第35回 カップルの同意を前提に少子化を考える
- 第36回 携帯電話の普及が競争と企業成長の号砲を鳴らす――インド・ケーララ州の小舟製造業小史
- 第37回 一夫多妻制――ライバル関係が出生率を上げる
- 第38回 イベント研究の新しい推計方法――もう、プリ・トレンドがあると推計できない、ではない
- 第39回 伝統的な統治が住民に利益をもたらす――メキシコ・オアハカ州での公共財の供給
- 第40回 なぜ勉強をさぼるのか？ 仲間内の評判が及ぼす影響
- 第41回 戦争は増えているのか、減っているのか？
- 第42回 安く買って、高く売れ！
- 第43回 家族が倒れたから薬でも飲むとするか――頑固な健康習慣が変わるとき
- 第44回 知識の方が長持ちする――戦後イタリア企業家への技術移転小史
- 第45回 失われた都市を求めて――青銅器時代の商人と交易の記録から
- 第46回 暑すぎると働けない!? 気温が労働生産性に及ぼす影響
- 第47回 最低賃金引き上げの影響（その3）アメリカでは（皮肉にも）人種分断が人種間所得格差の解消に役立ったらしい
- 第48回 民主主義の価値と党派的な利益、どっちを選ぶ？――権力者による民主主義の侵食を支える人々の行動
- 第49回 経済的ショックと児童婚――ダウリーと婚資の慣習による違い
- 第50回 セックスワーク犯罪化――禁止する意味はあるのか?
- 第51回 妻が外で働くことに賛成だけど、周りは反対だろうから働かせない
- 第52回 競争は誰を利するのか? 大企業だけが成長し、労働分配率は下がった
- 第53回 農業技術普及のメカニズムは「複雑」
- 第54回 女の子は数学が苦手？――教師のアンコンシャス・バイアスの影響
- 第55回 マクロ・ショックの測り方――バーティクのインスピレーションの完成形
- 第56回 女性の学歴と結婚――大卒女性ほど結婚し子どもを産む⁉
- 第57回 政治分断の需給分析――有権者と政党はどう変わったのか
- 第58回 賄賂が決め手――採用における汚職と配分の効率性
- 第59回 いるはずの女性がいない――中国の土地改革の影響
- 第60回 貧すれば鋭する？
- 第61回 貿易自由化ショックとキャリア再建の男女格差――仕事か出産か
- 第62回 最低賃金引き上げの影響（その4）――途上国へのヒントになるか？ ドイツでは再雇用によって雇用が減らなかったらしい
- 第63回 貧困からの脱出――はじめの一歩を大きく
- 第64回 大学進学には数学よりも国語の学力が役立つ――50万人のデータから分かったこと
- 第65回 インドで女性の労働参加を促す――経済的自律とジェンダー規範
- 第66回 所得が中位以上の家庭から保育園に通うと知的発達が抑えられます――イタリア・ボローニャ市の場合
- 第67回 男女の賃金格差の要因 その1──女性は賃金交渉が好きでない
- 第68回 男女の賃金格差の要因 その2――セクハラが格差を広げる
- 第69回 ジェンダー教育は役に立つのか
- 第70回 なぜ病院へ行かないのか？──植民地期の組織的医療活動と現代アフリカの医療不信
- 第71回 貧困層向け現金給付政策の波及効果
- 第72回 社会的排除の遺産──コロンビア、ハンセン病患者の子孫が示す身内愛
- 第73回 家庭から子どもに伝わる遺伝子以外のもの──遺伝対環境論争への一石
- 第74回 チーフは救世主？ コンゴ民主共和国での徴税実験と歳入への効果
- 第75回 権威主義体制の不意を突く──スーダンの反体制運動における戦術の革新
- 第76回 紛争での性暴力はどういう場合に起こりやすいのか？
- 第77回 最低賃金引き上げの影響（その5） ブラジルでは賃金格差が縮小し雇用も減らなかったが……
- 第78回 なぜ売買契約書を作成しないのか？ コンゴ民主共和国における訪問販売実験
- 第79回 国際的な監視圧力は製造業の労働環境を改善するか？ バングラデシュのラナ・プラザ崩壊のその後
- 第80回 民主化で差別が強化される？――インドネシアの公務員昇進にみるアイデンティティの政治化
- 第81回 バングラデシュのラナ・プラザ崩壊のその後(2)――事故に見舞われた工場に発注をかけていたアパレル小売企業は、事故とどう向き合ったのか？
- 第82回 児童婚撲滅プログラムの効果
- 第83回 公的初等教育の普及、それは国民を飼い慣らす道具──内戦による権力者の認識変化と政策転換
- 第84回 先生それPハクです──なぜ実証研究の結果はいつも「効果あり」なのか?
- 第85回 教育の役割──教科書は国籍アイデンティティ形成に寄与するのか
- 第86回 解放の甘い一歩
- 第87回 途上国の医療・健康の改善のカギは「量」か「質」か
- 第88回 人種扇動的レトリックの使用と国家の安定性──ドナルド・トランプの政治集会が黒人差別に与えた影響
- 第89回 都合が良ければ「民主的」、そうでなければ「非民主的」──政治的行動に対する知覚バイアスを探る