IDEスクエア
コラム
第4回 選手とコーチはずっと知っていた――打てば入るホットハンドは信じていい
PDF版ダウンロードページ： http://hdl.handle.net/2344/00051451
2019年8月
（5,715字）
われわれは純粋にランダムな現象にもパタンや規則性を見出し、意味づけをしてしまいがちである。飛行機のオーバーブッキングで座席がアップグレードされ、チェックインした先のホテルの部屋もアップグレードされると、夕食では無料のデザートがサービスで来ると考えてしまうかもしれない。
バスケットボールではシュートが数本入ると、その後、立て続けに入ることがある。この現象を指す言葉がホットハンドだ。有名なものは、2015年にNBAでクレイ・トンプソンが12分間に37点をあげた試合である。彼のチームメイトで稀代のシューター、ステフ・カリーでさえ、(ディフェンス陣の間に)陽の差す隙間があればシュートを打って点が入ると思った、と語ったほど。あの12分間、トンプソンは誰にも止められないホットハンドを確かに持っていた。
選手やコーチ、そして市井の観客が疑いもしないホットハンド現象を、心理学者グループが1985年の論文において統計的に検定した。心理学者たちは、「シュートを入れた直後のシュート」と「シュートをミスした直後のシュート」の成功率を比べた1。その差は3%ほどで、統計学的にはゼロと見做すことができた。つまり、心理学者は、ホットハンドは仮にそう見えたとしても、偶然の積み重ねと区別できないと結論した。人間は存在しないものを見てしまう傾向がある、とも。それ以来、研究者や学識あるスポーツ解説者は、ホットハンドに対して、「神話」だとか「よく知られているが認知過誤」と説明するようになり、これが正しい理解とされた。
ところが、もう一度、正しい理解が変わってしまう。ミラーとサンフルホは、2018年の論文で、「シュートを入れた直後のシュートの成功率qは、1本目のシュートの成功率pよりも必ず低くなる」ことを証明したのである2。シュート成功直後の成功率の理論値をqとすると、いわゆるベルヌーイ試行のp、つまり、疲れや相手チームの影響などを受けない機械のようなベルヌーイ選手の成功率pよりも、qは必ず低くなる。
心理学者たちは、実際の観測値がこのqよりも高くなるか検定すべきだったのに、qより高いpよりも高くなるかを検定してしまった。そのために、実際の観測値がqを越えていても「シュートを入れた直後のシュート」と「シュートをミスした直後のシュート」には差がないという結論に至ってしまった。1本目のシュートの成功率pと上記の理論値qの差p-qを加えると、かつて1985年の心理学者の論文の観測値では3%の超過成功率だったものは、正しくは12%の超過成功率となる。この値がゼロである確率は1%未満なので、本論文では、ホットハンドが「神話」である確率は1%未満と結論づけている。
成功直後の成功率qが1本目の成功率pよりも低くなることを理解するにはベイズの定理が枢要である。ベイズの定理とは統計学の定理で、物事が起きる前の確率と起きた後の確率の関係を示す奥深い式だ。試合前のウォームアップとして、以下のベイズの定理が成り立つことを無条件に受け入れてほしい。
Sが起こったときにAが起きる確率
ここでAをBという文字に入れ替えよう。
Sが起こったときにBが起きる確率
そのまま両辺の比を取ると以下のようになる。
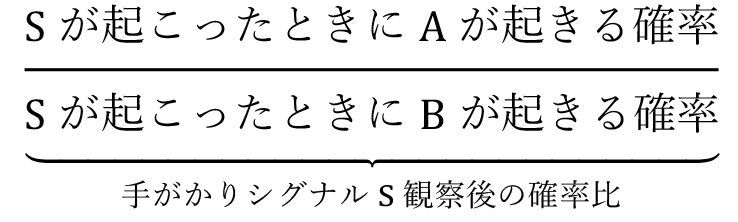
式(3)は情報のない「まっさら状態の確率比」
と「手がかりシグナルS観察後の確率比」である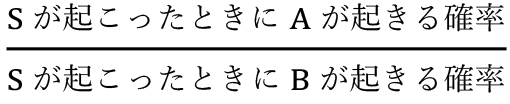
の関係を示している。
著者たちの別論考の例を使って具体的に考えてみよう3。第1クォーター開始。たとえば、あなたは厨房で働いていて、お客にアンが来る(Aが起きる)のか、ボブが来る(Bが起きる)のか、あなたには見えないとしよう。アンは100あるメニューをすべて均等に注文する。一方、ボブは偏食でサバ定食しか絶対に頼まない。アンもボブも同じ確率で来店し、他に客は来ない。つまり、客はアンである確率も、客はボブである確率も1/2だから、まっさらの状態の確率比は1。そして届いた注文はサバ定食(Sが起きる)。客はどっちだろう。
普通の感覚だと、どう考えてもボブだ。ボブがサバ定食を頼む確率(Bが起こったときにSが起きる確率)は1。アンがサバ定食を頼むのは100回に1回、つまり、Aが起こったときにSが起きる確率(=1/100)なので、ボブの確率が圧倒的に高いはずだ。そして、この答えも、この考え方も正しい。
第2クォーター開始。先の式の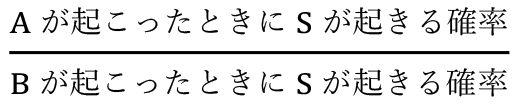
をベイズ因子というが、この分数はAがBよりもSというシグナルを相対的に与えやすい程度を示している。この例でのベイズ因子は(1/100)/(1)=1/100。つまり、アンが来ているときにSが起きる確率はボブが来ているときにSが起きる確率の1/100。よって、上の公式からすると、「届いた注文がサバ定食であった」という手がかり観察後の確率比はアンが来ている確率をまっさら状態の1/100に引き下げる。アンが厨房に与えられる手がかりはサバ定食以外に99種類あるので、サバ定食という手がかりが選ばれる可能性は低くなる。
ここでベンチのボブに選手交代。アンと違って、偏食ボブの与える手がかりは1つに制約されている。ボブのように手がかりの選択肢が制約されている現象がある場合、そのうちから手がかり(サバ定食)が選ばれたら、選択肢が制約されていない現象(アンの来店)よりも選択肢が制約されている現象(ボブの来店)が起こっている可能性が高いはずだ。
ここで鍵となるのが、先ほどのベイズ因子である。「AがSという手がかりを相対的に与えやすい」というベイズ因子が小さくなれば、式(3)の左辺の手がかり観察後の確率比は低下し、手がかり観察後に推論されるAが起こる可能性も相対的に低くなる。
第3クォーター開始。話を本筋のホットハンドに戻そう。A, B, Sを次のように読み替えてみる。Aはシュート成功、Bはシュート失敗で、SはS回目のシュートが吟味対象に選ばれることとしよう。S回目のシュートを吟味対象に選んだとき、シュートは成功(Aが起きた)か、失敗(Bが起きた)かのどちらかだ。そして実は、S回目のシュートが成功しているときにS回目のシュートが手がかりに選ばれる確率は、S回目のシュートが失敗しているときにS回目のシュートが手がかりに選ばれる確率よりも低い。なぜならば、S回目に成功している世界では、S回目とS+1回目を連続成功の吟味対象に選ぶことができるのに対し、S回目に失敗している世界ではS+1回目は連続成功を吟味する対象に選べないからだ。成功して吟味可能な対象が多ければ特定のS回目が選ばれる確率は低くなる。こうして、S回目のシュートを選んだとき、右辺のベイズ因子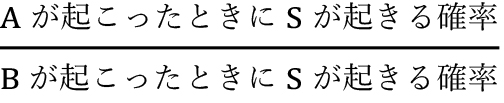
は1よりも小さくなって、左辺の手がかり観察後の成功確率比も低くなる。
気をつけるべきは、ホットハンド＝連続成功を吟味しようという研究設計がサンプル選択を歪めていることだ。仮に、S回目にシュートが成功すると、S+1回目もホットハンドのデータとして利用できる。反対にS回目のシュートが失敗すると、当然S+1回目はデータから排除される。よって、S回目に成功すると失敗したときにはないS+1回目というデータが余分にある。このため、S回目が成功しているとデータは吟味対象に選ばれる確率が下がる。アンは与えられる手がかりが多いために、サバ定食という手がかりをアンが与える確率はボブよりも下がるのと同じである。
相手チームのコーチがタイムアウトをとったようだ。その合間に作戦を再確認しよう。シュート総回数が3回で初回に成功したデータがあるとする。1回目に成功しているので、連続成功しているとすれば2回目と3回目のシュートだ。吟味対象に2回目を選んだ(S=2である)場合を考えると、2回目に失敗しているときは2回目のデータに選択肢が制約されるのに対し、2回目に成功しているときは吟味対象の選択肢には3回目のデータも含まれる。2回目成功のときは2と3回目が連続成功の吟味対象になり得るので、2回目が吟味対象になる確率は1/2。2回目に失敗していれば2回目のデータだけが連続成功の吟味対象になり得るので、2回目が吟味対象になる確率は1だ。失敗している方が連続成功の吟味対象に選ばれやすいのだ。ベイズ因子は1よりも小さくなる。
優勢に試合を運びながら第4クォーター開始。シュート成功率がpの選手のまっさらの確率比はシュート成功とシュート失敗の比、つまりp/(1-p)だ。S回目のシュートをホットハンドの吟味対象にすると、成功する場合よりも失敗する場合の方が吟味対象になる確率が高いので(=ベイズ因子が1未満)、S回目のシュートを吟味対象にするという手がかり観察後のシュート失敗確率は上がり、シュート成功確率は下がる。だから、連続したシュート成功確率はpよりも低いqになる。厨房にサバ定食の注文がきたとすると，アンよりもボブの方がサバ定食を注文する確率が高いので(=ベイズ因子が1未満)，サバ定食の注文を観測した後のボブ来店確率は上がり，アン来店確率は下がる。計量経済学ふうに表現すると、ホットハンド検定には前回成功したシュート回のみを吟味対象にするという標本選抜(ストリーク・セレクション)が自動的に埋め込まれている。このことに気付かずにいると、歪んだ検定になって誤った結論を導いてしまう。試合終了。
スポーツ好きの自称インテリたちに少なからずの驚きを持って迎えられたミラーとサンフルホ論文の衝撃は、当の選手やコーチには及んでいないかもしれない。1985年の論文が「神話」を否定したとき、ボストンの黄金時代を築いた名コーチ、レッド・オウアバックは関係ナッシングとばかりにこう言い放った。「こいつは誰だ? 研究をしたそうだ。気にする必要を全く感じない。」現場の選手もコーチもホットハンドを変わらず信じているのに、外野が勝手に否定して、外野が30年後に再び勝手にその間違いを修正しただけ、と思っているかもしれない。
でも、ミラーとサンフルホがこの発見に至るまでの経緯を知れば、オウアバックも少しは見直すのではないだろうか。彼らはシュート成功直後の成功率を計算し、この名選手の成功率がこんなに低いわけがないと思い、いくつもパタンを吟味して一貫して低い値が出ることを発見し、何かあると確信したそうだ。直感の鋭さと確信を理論に引き上げる知的な馬力、そして、何よりも一見しただけでおかしいと思えるほどゲームへの愛着があるからこそ、ホットハンドの証拠を示すことができたのだ。
一般的な教訓として、連続する事象を取り上げるとき、研究者は本論文の知見を活かすべきである。もっと一般的な教訓としては、ミラーとサンフルホ論文は長年プロとして携わってきた現場の感覚に敬意を払うこと、研究方法に対する謙虚さなどを訴えているように思える。当たり前になっていた知見に疑問を呈し、緻密な作業を経て常識を覆した著者たちに学ぶ点は多い。
＊この記事は「途上国研究の最先端」の番外編です。
写真1の出典
- Keith Allison, Klay Thompson of Golden State Warriors shooting against Jared Dudley of Washington Wizards, via Wikimedia Commons［CC-BY-SA-2.0（https://creativecommons.org/licenses/by-sa/2.0/deed.en）］.
著者プロフィール
伊藤 成朗（いとうせいろう）。アジア経済研究所 開発研究センター、ミクロ経済分析グループ長。博士(経済学)。専門は開発経済学、応用ミクロ経済学、応用時系列分析。最近の著作に"The effect of sex work regulation on health and well-being of sex workers: Evidence from Senegal."(Aurélia Lépine, Carole Treibichと共著、Health Economics, 2018, 27(11): 1627-1652)、主な著作に「開発ミクロ経済学」(『進化する経済学の実証分析』 経済セミナー増刊、日本評論社、2016年)など。
注
- ここでは理解を容易にするために簡単化したが、実際には心理学者たちは3本成功後の成功率と3本失敗後の成功率を比較している。Gilovich, T., R. Vallone, and A. Tversky. "The Hot Hand in Basketball: on the Misperception of Random Sequences," Cognitive Psychology, 1985, Vol.17: 295–314.
- Joshua B. Miller and Adam Sanjurjo, "Surprised by the Hot Hand Fallacy? A Truth in the Law of Small Numbers," Econometrica, 2018, Volume 86, Issue 6 (November): 2019-2047.
- 本稿の例は次の論文を踏襲している。Joshua B. Miller and Adam Sanjurjo. "A bridge from Monty Hall to the Hot Hand: Restricted choice, selection bias, and empirical practice," forthcoming, Journal of Economic Perspectives. この論文は直感的理解が難しいとされるモンティ・ホール問題も明快に解説していてお薦めである。