IDEスクエア
海外研究員レポート
出生率と女性の労働参加
PDF版ダウンロードページ:http://hdl.handle.net/2344/00049975
2008年12月
出生率と女性の労働参加との関係は、負の相関関係にあるとみなされてきた。1980年代までのデータを用いると、確かに負の相関が確認されるが、現在では、OECD諸国に関しては、正の相関にあるとされる(Brewster and Rindfuss 2000)。いずれにしても、出生率と女性の労働参加との間の因果関係ははっきりしておらず、現実には、両者は同時に決定されていると思われる。子供の数が増えれば、女性は労働参加を控えるだろうし、逆に、労働参加の増加は(とりわけ先進国では、教育水準の増加、離婚率の増加と相まって)、出生率の減少につながるだろう。労働経済学者は、女性の労働参加を出生率の関数と考えており、経済人口学者は、出生率の変化を女性の労働参加の関数と考えている。同時方程式体系にあるにもかかわらず、女性の労働参加を被説明変数、出生率を説明変数とするOLS推定値は、両者が正の相関にあれば過大評価で、負の相関にあれば過小評価で不一致となる。
労働経済学者は、出生率が女性の労働参加に与える効果について、不偏一致推定量を得るため、出生率を外生的に左右する操作変数を見つけることに腐心してきた。Angrist and Evans(1998)は、その代表的な例であり、二人以上子供がいる夫婦もしくは母親1を対象に、第一子と第二子の性別が異なるか否かを出生率の操作変数とした。彼らのアイデアは、子供が二人いる親は、二人の子供が同性であるよりは異性であることを好み、第一子、第二子が同性である親は第三子を望みやすいという事象を利用することである。第二子の性別が第一子の性別と合致するかどうかはランダムであるため、子供の性別そのものが女性の労働参加に直接影響を与えるわけではないが、第三子を産むかどうかの決定には影響を与えるだろうことを論拠に、操作変数としての妥当性を正当化している。
第一子と第二子の性別が妥当な操作変数であるためには、両者の性別が一致することが、第三子というかたちで子供の数が一人増えること以外の、観察不可能な変数をとおして女性の労働参加に影響を与えてはならない。Angrist and Evans(1998)は、USデータである1980年と1990年のCensus Public Use Micro Samples(PUMS)を用いて推定し、第一子と第二子の性別に内生性はないことを示している。しかしながら、アジアの文脈でも、それが妥当な操作変数として利用できるか否かは疑問である。第一子と第二子の性別そのものが女性の労働参加に影響を与えることはしばしば指摘される。例えば、女子が生まれると、家事労働の負担が減るため、女性の労働参加が増えるといったことである。本稿の目的は、Angrist and Evans(1998)が使用したと同じデータセットを用いて、アジア系サンプルに限り、第一子と第二子の性別を操作変数とした 2SLS推定法を用いて、出生率が女性の労働参加に与える影響を推定することである。とりわけ、Angrist and Evans(1998)の推定結果との違いと、操作変数の妥当性に着目している。
本稿の構成は以下のとおりである。第1節では、Angrist and Evans(1998)の推定モデルを紹介する。第2節では、母集団が異なる場合に、操作変数の妥当性がいかに影響を受けるかを議論し、アジア系サンプルを用いた推定結果を示す。第一段階の結果も示すことで、操作変数の説明能力がどの程度であるかも示す。同時に、フルサンプルを用いた結果も掲載するので、両者の比較が可能である。第3節は結びである。
第1節 2SLS 推定モデル
Angrist and Evans(1998)の主眼は、出生率が女性の労働参加に与える効果について、子供 の性別構成を操作変数とした推定である。彼らは、2SLS推定法について、主に二つの長所2を指摘している。一つは、労働参加に影響を与えると思われる共変量を加えることが可能となる。これらの共変量は、とりわけ操作変数の説明力の弱さの問題(=weak instruments)の可能性が高いときには重要である。もう一つは、操作変数である"Same sex"(=第一子、第二子が同性)は、"Two boys"(=第一子、第二子とも男子)と"Two girls"(=第一子、第二子とも女子)の二つの操作変数に分解できるため、過剰識別(=overidentified)2SLSモデルを設定することが可能となる。過剰識別制約(=overidentifying restrictions)の検定によって、モデル指定に誤差はないという帰無仮説が棄却されれば、操作変数"Same sex"の外生性が疑わしいことになる。変数"Same sex"が労働供給に与える影響のうち、子供の数が一人増えること以外の、観察不可能な理由がある場合には、操作変数の妥当性を正当化できないであろう。
Angrist and Evans(1998)は、2SLS推定モデルを以下のように設定している。第二段階の推定式は、
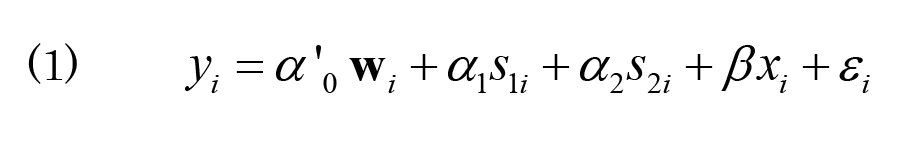
と表すことができる。Xiは、2人以上の子供がいるかどうかを表す内生変数であり、Wiは共変量3(母親の年齢、最初の子供が生まれたときの年齢)、S1iは第一子の性別、S2iは第二子の性別である。
第一段階の推定式は、
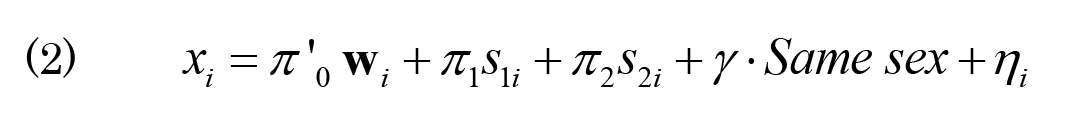
と表すことができる。変数"Same sex"は、第一子と第二子が同性であることを指す。
変数"Same sex"が、出生率のみならず労働供給量に影響を与える観察不可能な変数にも影響を与える場合は、変数"Same sex"が(1)式のεiと相関することとなり、操作変数としての妥当性が失われる。変数"Same sex"を操作変数"Two boys"と"Two girls"に分解することで、過剰識別制 約2SLSモデルを設定することが可能となる。
この第二段階の推定式は、
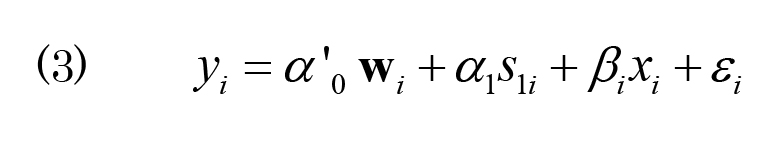
と表すことができる。過剰識別制約2SLSモデルでは、第二子の性別S2iを省いている。これは、 第一子、 第二子の性別の変数 S1i、S2iと、 操作 変数"Two boys"と "Two girls"は、
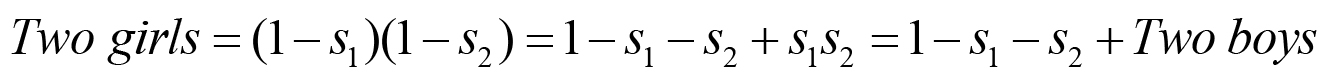
というように一次従属の関 係にあるため、S1iとS2iのどちらか一方を省く必要があるからである。操作変数を"Two boys"と "Two girls"としたときの第一段階の推定式は、
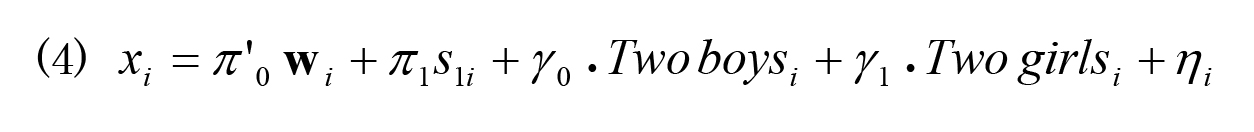
と表すことができる。変数"Two boys"、"Two girls"は、それぞれ第一子と第二子の性別が二人とも男子、女子であることを示す。
第2節 アジア系サンプルを用いた推定結果
フルサンプルでは、第一子と第二子の性別がともに女子である場合、男子である場合よりも、第三子をもつ選択をする(後に掲載の表1-2を参照のこと)。アジアのデータを用いた場合は、その可能性はさらに高まると予想される。子供の性別構成は、出生率のみならず労働参加にも異なる影響を与える可能性がある。操作変数"Two boys"、"Two girls"が労働供給量に対しても観察不可能な効果をもつようであれば、その妥当性は疑わしい。フルサンプルを用いた過剰識別制約の検定では、妥当性は棄却されなかったが(後に掲載の表 1-2 を参照のこと)、それが普遍的な結果であるかどうかは疑問である。例えば、南アジアでは、男子は親に対してより多くの金銭的利益をもたらすため、子供の性別や親の資金制約の差が、親の時間配分に異なる影響を与える(Rose 2000)とされる。この場合、子供の性別構成は、出生率のみならず、家族構成員の時間の価値、家計の生涯資産に大きな影響を与えるだろう。Chun and Oh(2002)は、Korean National Survey を用いて、第一子の性別を操作変数に、出生率が女性の労働参加に与える影響を推定した。彼らは、消費や教育費が第一子の性別によって変わらないことを根拠に、第一子の性別を操作変数とすることを正当化した。彼らによる 2SLS推定値はOLS推定値よりも絶対値が大きい。第一子が男子であると資産効果が働き、母親の労働参加を減少させる可能性も考えられる。仮に、男子を選好する母親であればあるほど、実際に男子を授かったときに労働参加をやめる可能性が高いならば、第一子の性別は妥当な操作変数ではないだろう。
親の、子供の性別に関する選好は、経済成長の度合い、文化、慣習など複雑な要因が絡み合って影響を受けるだろうが、男子を好む一つの要因として、アジアの文化的背景も考えられる。 本稿では、以上のことをモチベーションに、1980年PUMSのアジア系男性、女性をサンプルとして、(1)式、(3)式について2SLS推定を行った。仮に、男子をもつことが観察不可能な変数によって親の労働供給に影響を与えるならば、アジア系サンプルにおいては、変数"Two boys"、"Two girls"、従って"Same sex"も妥当な操作変数ではないだろう。
表1-1 は、第一段階の推定結果を表したものであり、(2)式、(4)式に相当する。表1-2はフルサンプルを用いた結果であり、比較のために添付している。アジア系女性が第一子、第二子 と同性の子供をもつと、アメリカ人女性全体の平均より、第三子をもつ可能性が高いことが分かる。両者で最も際立った違いは、第一子、第二子ともに男子である場合と、女子である場合に、第三子をもつ可能性の違いである。婚姻女性に限ると、"Two girls"の係数推定値はアジア系では0.1536である一方、アメリカ人全体では0.0801である。さらに、"Two boys"の係数推定値は、アメリカ人全体では有意であるが、アジア系に限ると有意ではない。
表2-1は、(1)式、(3)式に対応した2SLS推定結果を示している。比較のため、表2-2はフルサンプルを用いた結果である。いずれのサンプルでも、OLS推定値では、出生率が労働参加に及ぼす効果は、所得への効果を除き、有意に負である。一方で2SLS推定値では、アジア系サンプルはフルサンプルと比べ、以下に指摘するとおり異なる結果を示している。第一に、全ての2SLS推定値は5%水準で非有意となっている。アジア系女性全体では、"Worked for pay"(=センサスの前年に賃金のために働いたか否か)、"Weeks worked"(=センサスの前年に働いた週数)、"Hours/week"(=センサスの前年、週平均の労働時間)への効果が、アジア系婚姻女性に限ると"Worked for pay"への効果が 10%水準で有意である。第二に、これらの10%水準で有意であ る効果のみに着目すると、第三子の女性労働供給への負の効果は、アジア系女性でより大きく、アメリカ人女性全体との差は2倍である。例えば、第三子がいるアジア系の女性はいない女性より、年間で12.1 週間労働時間が少ない一方、アメリカ人全体では5.63週間少ないのみである。
第三に、アジア系サンプルでの推定値が、操作変数が"Same sex"である場合と、"Two boys"、"Two girls"である場合では格段に異なる一方、フルサンプルではさほど変わらないことである。表2-1では、操作変数を"Same sex"としたときの推定値はすべて非有意で、とりわけ対応する"Two boys"、"Two girls"を操作変数としたときの推定値が 10%水準でも非有意である場合には、絶対値も小さく、ときには符号すら異なる。親が子供の性別について強い選好をもつ場合には、変数"Same sex"は観察不可能な変数を介して労働供給に影響を与える可能性が高く妥当な操作変 数ではないだろう。
第四に、10%水準で有意となる2SLS推定値は、すべて対応するOLS推定値より絶対値が大きく、少なくとも 1980年代までは出生率と女性の労働参加との間に負の相関が認められている という点からは奇異に思われる。アジア以外の先進国のデータを使った同様の推定では、2SLS推定値は、通常OLS推定値より絶対値が小さく、ときにはゼロとの有意差がない(Iacovou 2001)。
第五に、過剰識別制約の検定は非説明変数がいずれの場合であっても棄却されない。これ は、"Two boys"、"Two girls"が労働供給モデルにおいて外生変数であることを示唆している。したがって"Two boys"を操作変数としても害は小さいだろうが、表1-1で分かるとおり、変数"Two boys"は出生率についてはさほど有益な情報をもっていないだろう4。
最後に、表2-1のコラム(8)、(9)をみると、出生率は夫の労働供給に影響を与えない。推 定値の絶対値はフルサンプルと比較して大きいが、標準誤差もそれ以上に大きいため、出生率の 効果を性格に推定することはできない。
第3節 結び
子供の性別構成が操作変数として妥当か否かは、性別構成が観察不可能な理由を通して労働供給に影響を与えるか否かによる。アジアの一部の文脈では、親の男子に対する選好が伝統的に指摘されてきた。本稿では、1980年PUMSのアジア系サンプルを使い、アメリカ人フルサンプルとの比較を試みた。アジア系サンプルを用いた2SLS推定値は10%水準で有意となるのみであったが、その絶対値はフルサンプルの2倍であった。第一段階の推定式では、第一子、第二子ともに男子であることは、第三子をもつ選択に何の影響も与えないが、ともに女子であることは 強い影響力をもつことが分かった。操作変数"Two boys"、"Two girls"を用いた過剰識別制約の検定では、モデル指定の誤差は棄却されなかったが、本稿で示した結果は、異なる文化背景がある場合に、これらの操作変数を用いる際には注意が必要であることを示唆している。
表1-1:第一段階推定、"Same sex"が出生率に与える影響、 1980年 PUMS アジア系サンプル
| 説明変数 | 婚姻女性 | |||||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
|
Boy 1st (=第一子が男子) |
– | -0.0466 | 0.0052 |
– |
-0.0412 |
0.0196 |
| (0.0133) | (0.0186) |
|
(0.0140) |
(0.0196) |
||
|
Boy 2nd (=第二子が男子) |
– | -0.0517 | – |
– |
-0.0607 |
– |
| (0.0133) |
|
(0.0140) |
|
|||
|
Same sex (=第一子、第二子が同性) |
0.0832 | 0.0820 | – | 0.0906 |
0.0929 |
– |
| (0.0143) | (0.0133) | (0.0151) |
(0.0140) |
|
||
|
Two boys (=第一子、第二子が男子) |
– | – | 0.0302 | – |
– |
0.0321 |
| (0.0185) |
|
(0.0195) |
||||
|
Two girls (=第一子、第二子が女子) |
– | – | 0.1337 | – |
– |
0.1536 |
| (0.0191) |
|
(0.0202) |
||||
| その他の共変量を含むか? | No | Yes | Yes | No |
Yes |
Yes |
| R2 | 0.0072 | 0.1509 | 0.1509 | 0.0087 |
0.1458 |
0.1462 |
注:括弧内は標準誤差。その他の共変量は"Age"(=母親の年齢), "Age at first birth"(=初産の年齢) を指す。サンプルは 1980年PUMSにおいて、人種がアジア系と分類された男性、女性に限っている。サンプル・サイズは、全女性(子供を二人以上もつ 21‐35歳の女性)については 4,525人、うち婚姻女性については4,021人である。
表1-2:第一段階推定、"Same sex"が出生率に与える影響、1980年 PUMS フルサンプル
| 説明変数 | 婚姻女性 | |||||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
|
Boy 1st (=第一子が男子) |
– | -0.0082 | 0.0001 |
– |
-0.0109 |
0.0006 |
| (0.0015) | (0.0021) |
|
(0.0018) |
(0.0026) |
||
|
Boy 2nd (=第二子が男子) |
– | -0.0083 | – |
– |
-0.0115 |
– |
| (0.0015) |
|
(0.0018) |
|
|||
|
Same sex (=第一子、第二子が同性) |
0.0585 | 0.0601 | – | 0.0664 |
0.0686 |
– |
| (0.0016) | (0.0015) | (0.0019) |
(0.0018) |
|
||
|
Two boys (=第一子、第二子が男子) |
– | – | 0.0518 | – |
– |
0.0572 |
| (0.0021) |
|
(0.0026) |
||||
|
Two girls (=第一子、第二子が女子) |
– | – | 0.0684 | – |
– |
0.0801 |
| (0.0021) |
|
(0.0026) |
||||
| その他の共変量を含むか? | No | Yes | Yes | No |
Yes |
Yes |
| R2 | 0.004 | 0.097 | 0.097 | 0.005 |
0.091 |
0.091 |
注:括弧内は標準誤差。その他の共変量は"Age", "Age at first birth"、人種ダミー(黒人、ヒスパニック、白人以外その他の人種)を指す。サンプルは1980年PUMS、子供を二人以上もつ 21-35歳の女性である。サンプル・サイズは、全女性が386,537人、うち婚姻女性が 228,997人である。
表2-1:労働供給モデルのOLS/2SLS推定、1980年PUMSアジア系サンプル
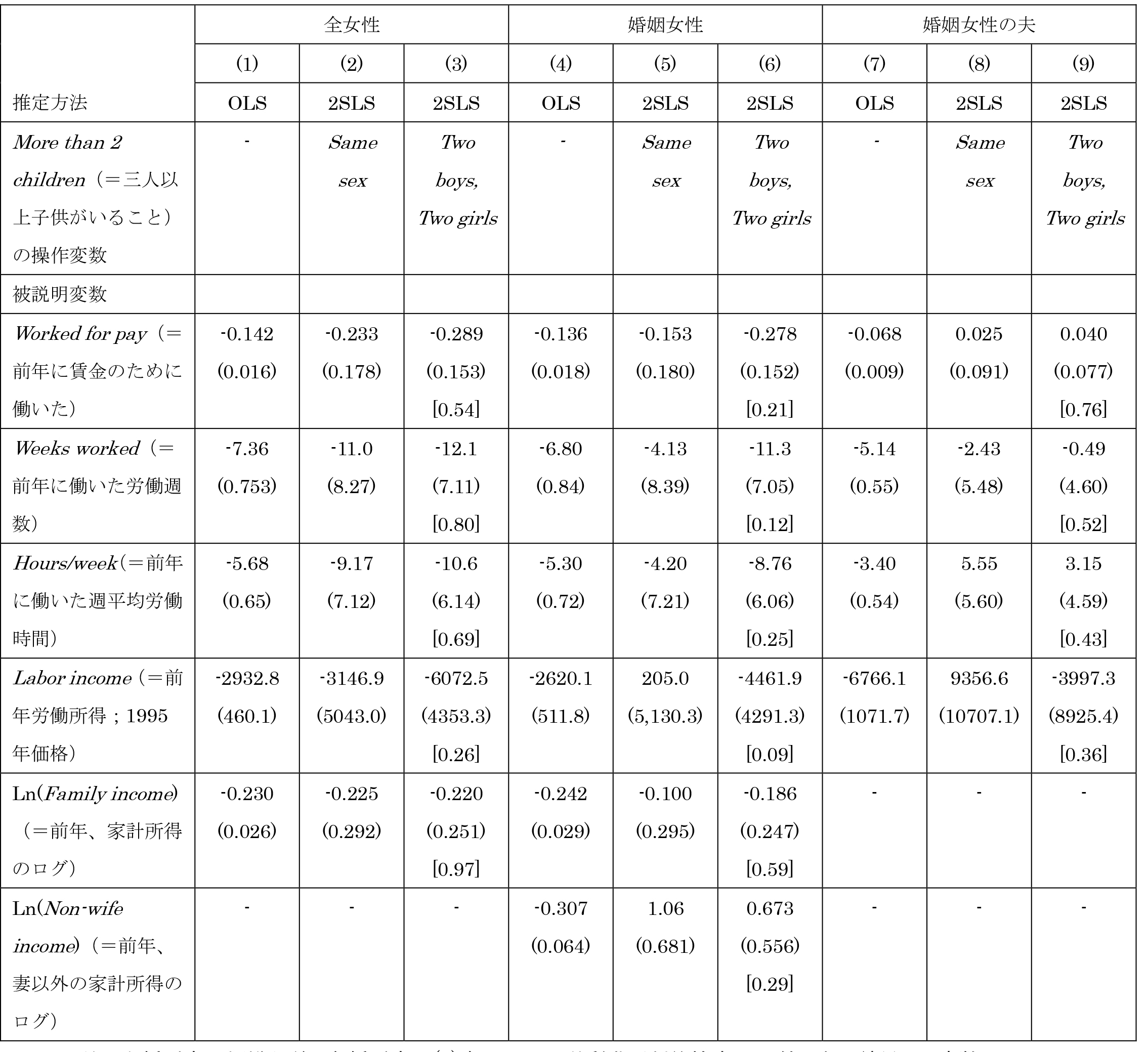
注:丸括弧内は標準誤差。角括弧内は(3)について過剰識別制約検定の p-値。表の結果は、変数"More than 2 children"の係数推定値である。コラム(2)、(5)、 (8)は本文の(1)式に対応する。コラム(3)、 (6)、(9) は本文の(3)式に対応する。その他の共変量は、"Boy 1st", "Boy 2nd", "Age", "Age at first birth"であり、コラム(3)、(6)、 (9)は"Boy 2nd"を除いている。サンプルは表 1-1と同様である。
表2-2:労働供給モデルのOLS/2SLS推定、1980年PUMSフルサンプル
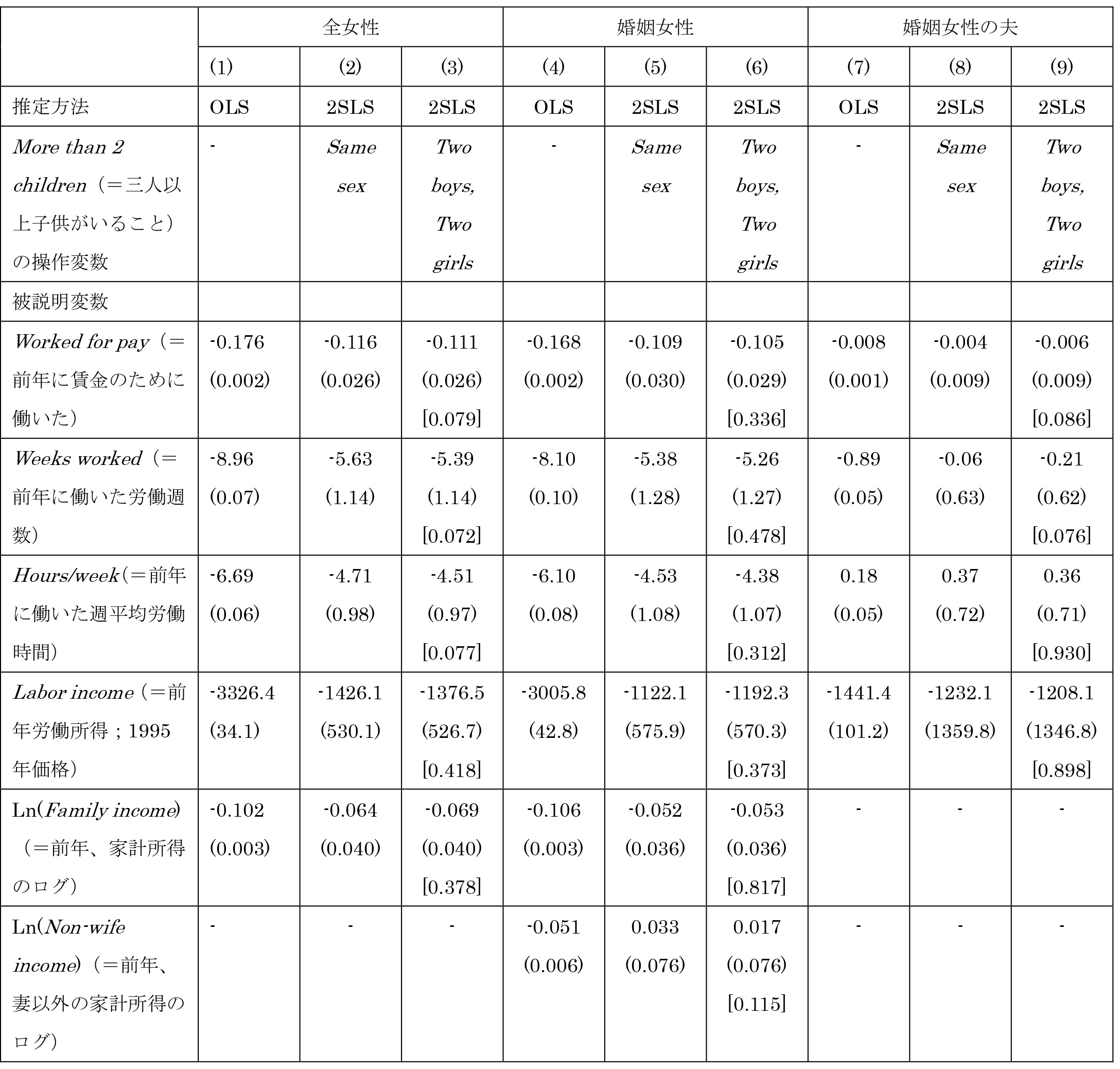
注:丸括弧内は標準誤差。角括弧内は(3)式について過剰識別制約検定のp-値。表の結果は、変数"More than 2 children"の係数推定値である。コラム(2)、(5)、 (8)は本文の(1)式に対応する。コラム(3)、(6)、(9) は本文の(3)式に対応する。その他の共変量は、"Boy 1st"、"Boy 2nd"、"Age" "Age at first birth"、人種ダミー(黒人、ヒスパニック、白人以外その他の人種)であり、コラム(3)、(6)、(9)は"Boy 2nd"を除いている。サンプルは表 1-2と同様である。
参考文献
- Angrist, D. Joshua and Evans, William N. (1998) 'Children and Their Parents' Labor Supply: Evidence from Exogenous Variation in Family Size', American Economic Review, 88(3): 450-477.
- Brewster, Karin L. and Ronald R. Rindfuss. (2000) 'Fertility and Women's Employment in Industrialized Nations', Annual Review of Sociology 26: 271-86.
- Chun Hyunbae and Jeungil Oh (2002) 'An Instrumental Variable Estimate of the Effect of Fertility on the Labor Force Participation of Married Women', Applied Economic Letters, 9, 631-634.
- Iacovou, Maria (2001) 'Fertility and Female Labor Supply', Discussion Paper. IS, University of Essex, Colchester, UK.
- Rose Elaina (2000) 'Gender Bias, Credit Constraints and Time Allocation in Rural India', Economic Journal, 110(465): 738-758.
脚注
- Angrist and Evans(1998)のデータセットであるCensus Public Use Micro Samples(PUMS)では、遡って何人子供を産んだかという出生率に関する情報はない。代わりに、各家庭で報告される子供の数を、母親の"Fertility"とみなしている。そのために彼らのサンプルは、年齢が21-35歳の二人以上の子供がいる女性に限っている。35歳以下であれば、最年長の子供が18歳以上である可能性、つまり一人立ちしている可能性は低く、また、21歳以下の女性が三人以上の子供をもつ可能性が低いからである。
- Angrist and Evans(1998)は、厳密には三点の長所を指摘している。残りの一つは、子供の性別の追加的効果をコントロールできることである。しかし、追加的効果は、さほど重要でなく、実際に表 1-2 に見られるとおり、操作変数である"Same sex"(=第一子、第二子が同性)を分解して"Two boys"(= 第一子、第二子とも男子)と"Two girls"(=第一子、第二子とも女子)を操作変数として用いると、追加的効果は説明力を失っている。
- Angrist and Evans(1998)では、すべての人種がサンプルに含まれるため、共変量に、人種ダミーも含んでいる。
- 試みに、"Two girls"のみを操作変数として2SLS推定を行ったところ、結果は"Same sex"を操作変数としたときの推定結果とさほど変わらなかった。これは、"Two boys"が2SLS推定において無害である一方、出生率にとって有益な情報をもっていないことから、予想通りの結果に思われる。


