IDEスクエア
海外研究員レポート
ワシントン大学経済学部博士課程の必修・計量経済学の課題
PDF版ダウンロードページ：http://hdl.handle.net/2344/00049987
2008年3月
経済学部博士課程の計量経済学の授業（担当教官：Prof. Richard Startz）では、必修コースであるため理論的な理解はもちろんのこと、論文を書く実践的なトレーニングもなされた。1クォーターで学生に要求された内容は、中間・期末試験のほか、理論的な理解を深め、また確認する課題（Greene（2008）の教科書の問題など）、そして論文2本という、かなり充実したものであった。
論文のテーマは自由に選べるわけではなく、それぞれ、経済学の著名な論文である、Hall（1978）、 Fama（1975）の検証をベースとした拡大論文であった。前者は、消費のランダムウォーク仮説を支持した論文であり、後者は、利子率を設定する市場の効率性を支持した論文である。これらの論文を検証するための課題が具体的に与えられ、その課題への回答を含んだ論文を書くことが求められた。消費のランダムウォーク仮説は、恒常所得仮説の一部であり、途上国の経済でも重要なテーマである消費の平準化とも関連する。以下では、前者を検証し拡大した課題論文の内容の部を紹介したい。
タイトル：消費のランダムウォーク仮説再考
I.はじめに
ケインズ消費関数の大きな問題点は、現在と将来の消費という時間の概念に欠けることである。経験的には、将来予想される消費が現在の消費行動に影響を与えることから、現在の消費は、生涯の所得によって決定されるという恒常所得仮説が提唱された。恒常所得仮説によれば、一時的な所得は、現在の消費に影響を与えず、消費は将来にわたって平準化されるはずである。
消費のオイラー方程式が、恒常所得仮説の中核にある。確率的オイラー方程式は、典型的な消費者が生涯の所得という制約のもとに予測される生涯の効用を最大化することによって求められる。消費効用関数が二次式で与えられ、実質利子率が一定であることを前提とすると、将来予測される消費は現在の消費によってのみ決定される。つまり、将来の消費を決定する変数は現在の消費以外になく、消費はランダムウォークに従う。合理的な消費者は、恒常所得に関するすべての情報（消費以外の変数）をもとに現在と将来の消費を決定するはずであり、将来の消費について予測不能な部分は、恒常所得に関する確率的なショックにのみ影響を受けるはずだからである。
本稿の目的は、消費、所得、（消費に影響を与える資産という意味での）株式の最新のデータをもとに、Hall（1978）の実証を再度行い、ランダムウォーク仮説を検証することである。消費を1期から4期のラグに回帰させると、1期ラグのみが有意であった。また、漸近的な解釈をすることが妥当か否かを検証するため、モンテカルロ・シミュレーションを行ったところ、本稿のサンプル数196が十分であることも分かった。所得のラグと株価指数のラグを説明変数に加えても、上記の結論にはほぼ影響を与えなかった。また、データの期間を60期にしぼり、それぞれの期間において同じ回帰を繰り返す方法（Rolling Window Regression: RWR）により、データ期間によって結論が影響を受けるか否かも検証したが、やはり違いはなかった。
また、消費の1期ラグ以外に説明力をもつ変数を探すという意図から、Index of Consumer Sentiment （ICS）を説明変数に加えた。ICS を加えた理由は、ICS が恒常所得の変化を反映すると考えたからである。仮に、消費の決定にあたり、情報がすべて利用されないのであれば、ICS のラグは消費ctの決定に説明力をもつはずである。ICSの1期ラグは消費ctを優位に説明したため、ランダムウォーク仮説は棄却された。
本稿の構成は以下のとおりである。Part IIIでは、Hallと同様の基本的な回帰を、最新のデ ータをもとに行い、ランダムウォーク仮説を検証する。モンテカルロ法は、加えて、実証結果が正しいか否かを検証する試みである。Part IVでは、推計結果が、データの期間によって異ならないか否かを調べるため、RWRを試みた。Part Vでは、ICSの1期ラグが現在の消費ctを決定するという結果を示している。Part VIでは、非定常時系列データ回帰に関する問題点について論じている。
II.データ
Figure 1は、1959年第1四半期から2007年第4四半期までの、四半期末の一人当たり消費（con_pc）、一人当たり可処分所得（inco_pc）、一人当たり株価指数＝S&P500指数（sp500_pc）をプロットしたものである。すべてのデータは、Economagicのウェブサイト（www.economagic.com）から入手し、2000年のUSドル価格に換算している。本稿の目的は、ランダムウォーク仮説を検証することであるため、消費データは、非耐久消費財・サービスのみを含んでいる。Hallは、「サービス・フローを耐久消費財のストックに帰するという方法は、人為的である」（Hall 1978, p.979）として、耐久消費財を考慮していない。これは、消費者が耐久消費財と非耐久消費財について、別個の効用関数を有していることを前提としている（Campbell and Mankiw 1990）ため、この前提が正しくなければ、耐久消費財も考慮しなければならない。本稿では扱わないが、耐久消費財の考慮は、今後の課題としたい。
図1：一人当たり消費、可処分所得、S&P500指数のトレンド
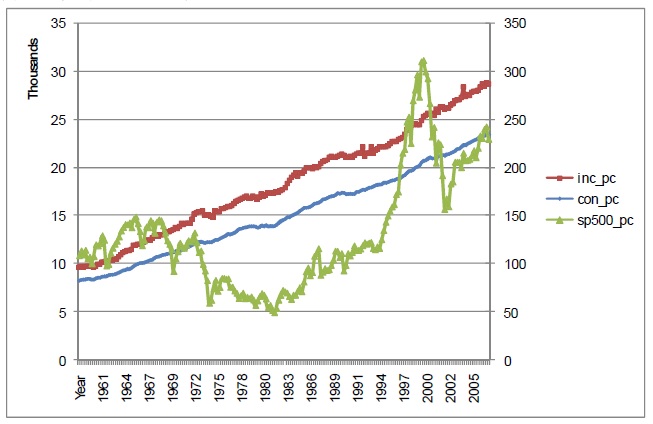
図1では、消費と可処分所得が似た動きを見せている。消費は可処分所得の一部であるが、動きはより安定している。ログをとった消費の標準偏差は0.30であるが、可処分所得のそれは0.75である。株価指数は予想通り変化が激しく、ショックに反応している。たとえば、オイルショック時の下落と、ネットバブル時の高騰を容易にみてとることができる。
III.基本的な実証結果とモンテカルロ法による検証
Hallの理論は、t-1期の消費の限界効用とt期の消費の予測される限界効用を等しくするオイラー方程式、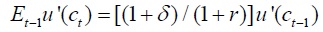
（δは主観的時間選好、rは実質利子率）に基づいている。消費者は、t-1期において分かっているすべての情報をもとに、予測される生涯の効用を最大化させるように、t-1期における消費を決定する。したがって、t-1期に分かっている情報のうち、消費水準を除いては、予測される限界効用に影響を与え、将来の消費ctを予測するに役立つ変数は存在しない。効用関数が二次式で与えられ、実質利子率が一定であることを前提とすると、限界効用は確実性等価の結果を得、限界効用関数は線形で与えられる。すなわち、消費者は消費の決定において恒常所得の平均のみをもとに決定し、分散は考慮しない。有名な理論的帰結は、消費はランダムウォークに従い、
c1=α+βct-1+ε1 （1）
式で与えられる。表1は、消費を1期ラグに回帰させた（1）式の結果である。係数の推定値は1.0027で、現在の消費は1期ラグと非常に高い相関関係にある。t値は822.5で強く有意にある。消費は0.3％の割合で伸びている。しかしながら、この結果を正しく解釈することは難しく（Romer 2006, p.357）、恒常所得仮説を正当化する十分な理由とはいえない。Hall自身、この結果は「消費が時系列に強く相関しているという、よく知られた事実の解釈に異ならない」（Hall 1978, p.980）と認めている。
表1：推計結果
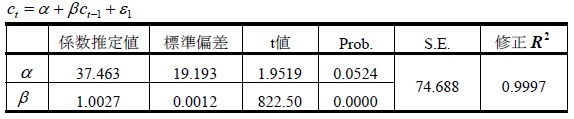
この回帰の大きな問題点は、統計の解釈が難しいことである。時系列データでは、OLS推定量のサンプル数に限りがある場合の仮定を満たすことが難しいため、誤差の漸近的正規分布、そのためにサンプル数が多いことを前提としている。しかしながら、本稿のサンプル数は、典型的な時系列データ同様、それほど多いわけではない。誤差の分布が明らかでないときに、検定統計を分析するためには、モンテカルロ法が役立つといわれる。なぜなら、「漸近的分布に依存しなくてもよいからである」（Campbell and Mankiew 1990, p.273）。本稿でのモンテカルロ法は、以下のデータ生成プロセス（DGP）である。
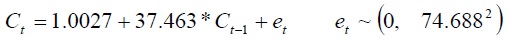
DGPで使用した数値は、表1で示した回帰の結果である。モンテカルロ法を利用して、50、200、1,000のサンプル数からなる消費データを生成し、それぞれのサンプル数について、データ生成を10,000回繰り返した。それぞれのデータ生成回において、係数α, βが真の値に等しいという帰無仮説について、t値を計算した。200のサンプル数では、5％水準での棄却率は、α, βについて、それぞれ6.21、7.29であった。サンプル数1,000では、棄却率はそれぞれ5.13、5.18、サンプル数50では、それぞれ6.21、7.29であった。回帰式（1）の統計的解釈が有効であるためには、棄却率は5％でなくてはならない。よって、サンプル数が50前後のときには、漸近的分布に依存することは問題であるが、本稿の198であれば、検定統計を解釈することがそれほど大きな問題とはならないことが分かった。
次に、過去の消費が将来の消費についての情報を有しているか否かを調べるため、消費の2～4期ラグを加えて回帰を行った。
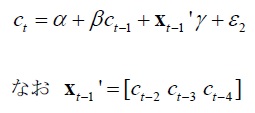（2）
結果は表2のとおりである。1期ラグct-1を除き、それ以上のラグは統計的に有意でない。また、2～4期ラグがまとめて説明力をもたないという帰無仮説を棄却することはできなかった。結果は、Hallの仮説を支持する。
表2：推計結果
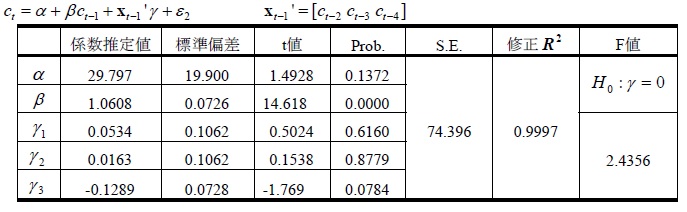
サンプル数が少ない場合の問題点は、F値についても当てはまるため、同様のモンテカルロ法によってF値の有効性を検証した。方法は、同様に50、200、1,000のサンプル数をそれぞれ10,000回生成することによって行った。それぞれの生成回において、帰無仮説γ=0についてF検定を行い、5％水準で棄却率を計算した。ここでも、サンプル数50では、漸近的に正規分布を仮定するには信頼性が足りないが、サンプル数200であれば、漸近的正規分布を仮定したうえでF値を信頼することが可能だろうという結論である。要するに、2期以上のラグは、消費を説明しないという結論は信頼性に足りるだろう。
Hallのランダムウォーク仮説は恒常所得仮説の枠組みにある。よって、所得のラグが消費 について説明力をもつか否かを検証する必要があるだろう。（2）式において、Xt-1を1～4期の可処分所得として回帰を行った。表3は、消費の1期ラグの係数は0.9999で統計的に有意であった。所得ラグの係数は4期ラグのマイナスを除いて、ほぼ有意でなかった。F値は1.43で、所得ラグは消費に対して全く説明力をもたないという帰無仮説を棄却しなかった。
表3：推計結果
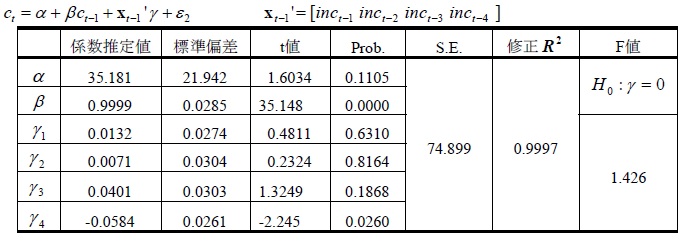
Hallは、株価指数の1～4期ラグが消費に対して説明力をもたないという帰無仮説を厳密な意味で棄却した。本稿もHallにならい、（2）式において、Xt-1を1～4期のS&P500指数として回帰を行った。消費の1期ラグは1.0012であり、統計的に有意であった。しかし、S&P500指数の係数は、4期ラグがマイナスであったほかは、統計的に有意でなかった。株価指数のラグが消費について説明力をもたない帰無仮説は、5％水準で棄却できなかった。
表4：推計結果
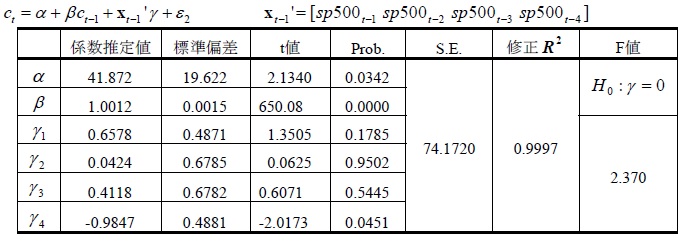
IV.パラメータの安定性
これまでの結果は、Hallの仮説を支持する。しかしながら、データの対象期間が異なれば、異なる結果とならないとは限らない。Hallの仮説が、データ期間の選択についても安定しているか否かを検証するため、60四半期を一つのウインドウ（よって最初のウインドウは1950年第1四半期～1973年第4四半期、二番目のウインドウは1959年第2四半期～1974年第1四半期……と続く）として回帰を繰り返すRolling Window Regression（RWR）を行った。
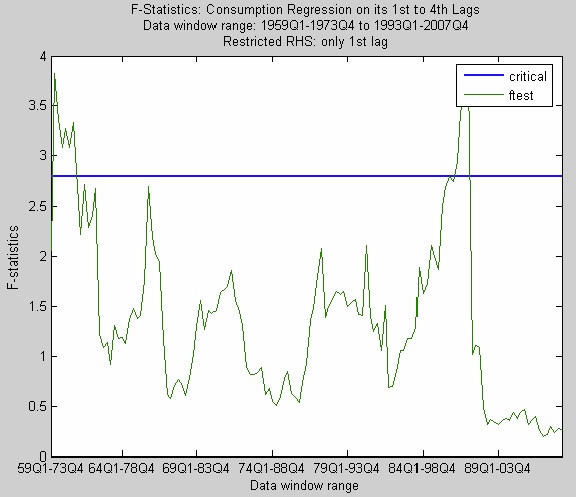
最初に、消費をその1～4期ラグに回帰させた。各ウインドウにおいて、1期ラグ以上のラグは消費について何ら説明力をもたないという帰無仮説について、F値を計算した。図2は、60ウインドウについて、F値をプロットしたものである。ほとんどのウインドウで帰無仮説を棄却することができず、Hallの仮説を支持している。
図2
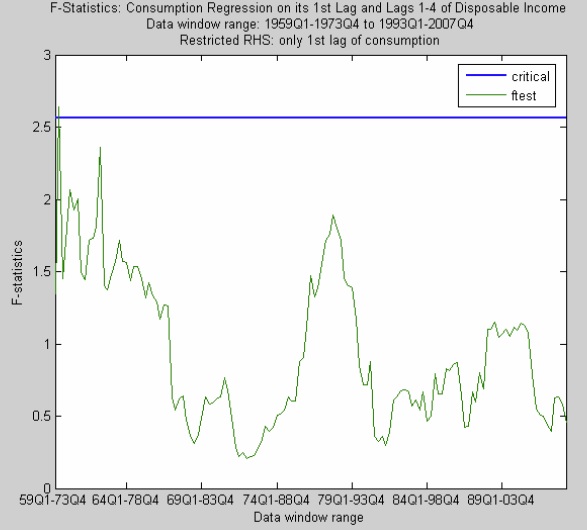
次に、消費を自身の1期ラグ、可処分所得の1～4期ラグに回帰させた。図3は、所得ラグが消費に対して何ら説明力をもたないとする帰無仮説に基づくF値をプロットした。図3に明らかなとおり、ほとんどのウインドウでは帰無仮説を棄却できず、Hallの仮説を支持している。
図3
最後に、消費を自身の1期ラグ、S&P500指数の1～4期ラグに回帰させた。Hallは、株価指数のラグは消費について説明力をもつという結果を示している。図4は、ほとんどのウインドウで、株価指数のラグは説明力をもたないという結果を示しており、Hallの結果とは異なる。本稿の結果は、消費の1期ラグ以外の変数は説明力をもたないというHallのもともとの仮説を支持するものである。帰無仮説を棄却している初期のウインドウは、Hallのデータ期間（1948年第1四半期～1977年第1四半期）と合致しており、Hallが株価指数について、帰無仮説を棄却したのは、データ期間に依るところが大きいかもしれない。
図4
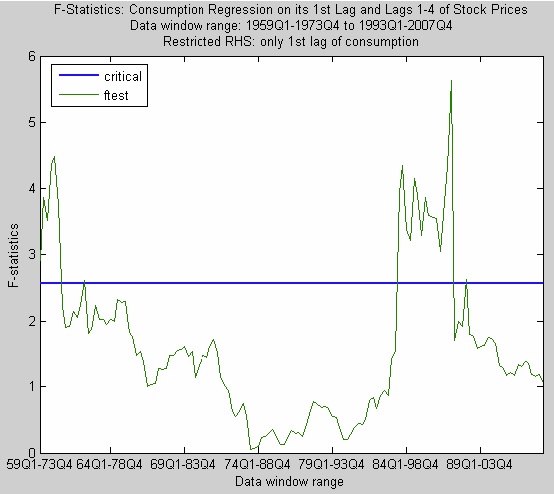
また、上記の結果は、Hallのいう修正ランダムウォーク仮説を支持するように思われる。Hallは、株価指数が消費と同様の動きを見せていることは、恒常所得仮説を支持するものであると主張している（Hall 1978, p.973）。Hallによれば、株価指数はランダムウォークに従うことが知られており、その動きは、恒常所得の変化を消費より素早く反映しているにすぎない、つまり、結果として消費に先行しているにすぎないという。株価指数に関する帰無仮説が棄却されたウインドウは、だいたい消費の2～4期ラグが棄却されたウインドウと合致している。仮に株価指数が恒常所得仮説を棄却するかたちで消費について説明力をもつならば、すべてのウインドウについて高いF値をもつはずである。しかし図4では、株価指数のラグは、ほとんどのウインドウにおいて説明力をもっていない。
V.新たな変数の試み：Index of Consumer Sentiment（ICS）
Hallの仮説を棄却するという意図をもって、t期の消費ctを予想する変数を加えてみたい。Hallによれば、合理的な消費者は、t－1期におけるすべての情報を利用して生涯の消費を平準化するため、t－1期においては、消費ct-1以外に現在の消費ctを説明する変数は存在しない。
非耐久消費財・サービスの消費は、アメリカのGDPの60％を占める。経済に占める消費の重要性に鑑み、効果的な政策立案のため、将来の消費を正確に予測することが試みられてきた。 消費の予測に関する直接的な変数としては、ミシガン大学のConsumer Survey Centerが月毎に集計しているIndex of Consumer Sentiment （ICS）を挙げることができよう。ICSについては、ウェブサイト（http://www.sca.isr.umich.edu）に詳しいが、簡潔にいうと、消費者の支払意欲を測る指標であり、実際、投資家や政府により、将来の消費を予測するために使われている。四半期末のICSデータは、1977年の第4四半期から入手可能だが、本稿の目的にとっては十分な長さであると思われる。ICSデータも他のデータ同様、2000年価格に換算した。
また、ICSには、Hallの論文の検証にあたって、説明変数として加えるにふさわしい理由があると考える。本稿は、前出のRWRがHallの修正ランダムウォーク仮説を支持する結果であることから、修正仮説の検証に関心がある。Hallによれば、現在の消費を過去の株価指数に回帰させると、過去の株価指数は一見したところ消費を説明するように見える。しかしながら実際は、両者ともランダムに動いており、たまたま多少のズレをもって同様の動きをしているにすぎない。この修正仮説を検証するには、恒常所得の変化を反映する変数が必要である。ICSは、消費者に対し、現在の所得状況のみならず、失業率やデフレの見込みなど、マクロ経済についての長期的な予測に関する質問をしており、この要件をみたす変数であるだろう。興味深いことに、質問事項には、消費者が現在を、耐久消費財を購入するタイミングと考えるか否かというものも含まれている。このような耐久消費財は、恒常所得を念頭において購入時期を考えるものである。よって、ICSは恒常所得の変化を説明すると考える。
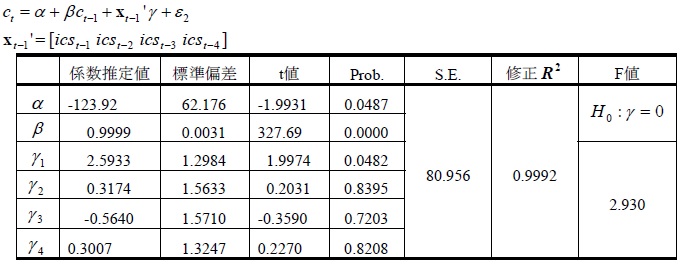
初めに、（2）式につき、Xt-1をICSの1～4期ラグとして回帰を行った（表5）。消費の1期ラグ係数はこれまでと同様有意であったが、その絶対値は1以下であり、Xt-1を株価指数の1～4期ラグ、消費の2～4期ラグとしたときと異なる結果であった。ICSの1期ラグ係数は2.59、F値も2.93と5％水準で有意であり、これもXt-1が株価指数のラグ、消費の2～4期ラグであったときと対照的な結果である。
表5：推計結果
ICSにつき、これまでと同様のRWRも試みた。予想に反し、ICSのラグはほとんどのウインドウで説明力をもたない（図5）。消費ct-1が一度決定されると、ICSのラグは消費ctについて説明力をもたないとの結果となった。
図5
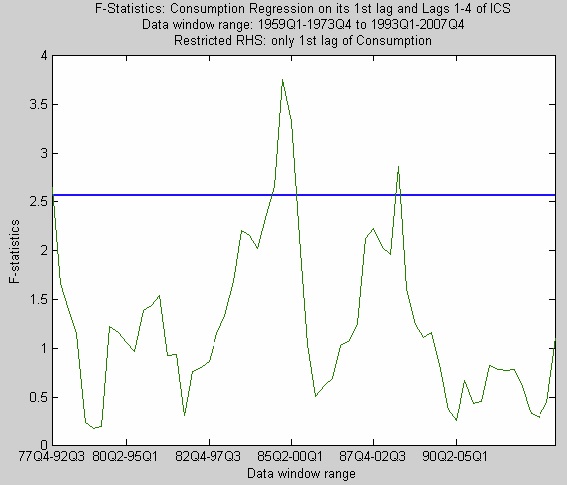
表5と図5との間で、相反する結果をいかに解釈すればよいのだろうか。RWRの結果では、データ期間によって係数の推定値が安定していないことが判明した。ただ、RWRでは、それぞれのウインドウのサンプル数が54しかないという欠点がある。本稿で行ったモンテカルロ法によれば、サンプル数50では、検定結果の解釈に問題があることが分かっている。RWRのF値の解釈は、サンプル数117の表5の検定結果より、信頼性が低いと考えられる。よって、表5の結果に重きを置き、ICSの1期ラグがt期の消費ctについて、何らかの説明力をもつと解釈し、Hallの仮説を棄却すると判断する。
このように、厳密な意味でのHallのランダムウォーク仮説は棄却されたが、修正仮説についても検証したい。ICSは恒常所得の変化を反映すると推測できる。仮に修正仮説が正しければ、株価指数はICSの関数のはずである。株価指数をICSのラグに回帰させると、係数は強く有意であった（係数推定値＝3.965, t値＝7.9716）。この結果は、株価指数のラグが消費ctについて説明力をもつのは、恒常所得の変化を消費よりも素早く反映しているにすぎないという修正仮説を支持するだろう。
サンプル数が少ないという問題点はあるものの、RWRのF値の動きに着目すると、ICSのラグについて帰無仮説が棄却されたウインドウは、株価指数のラグについて、また消費の2期以上のラグについて、棄却されたウインドウと対応している。Hallが株価指数の説明力について議論したと同様の議論がICSの説明力についても当てはまりそうである。すなわち、ICSは恒常所得の変化を反映すると考えられ、消費や株価指数のラグよりも素早く、恒常所得の変化に対応すると考えられる。もし、この仮説が正しければ、ICSのラグは現在の消費ctについて説明力をもつはずであり、これは、修正ランダムウォーク仮説、また恒常所得仮説と整合的である。
VI.非定常系列
もし、ランダムウォーク仮説が正しければ、消費の時系列は非定常となり、通常の検定統計は漸近的に正規分布とならないはずである。このことは、通常の検定結果の解釈について、注意が必要であることを示唆している。より正確に言えば、消費データが定常であればOLS推定量は漸近的に正規分布であり、通常の検定統計を使って係数推定値の有意性をチェックできるはずである。しかし、もし消費データが非定常であれば検定統計は正規分布であるという仮定は成り立たない。この問題点は、モンテカルロ法によって確かめることが可能である。モンテカルロ法によって定常と非定常の時系列データに関するDGPを試みた。まず、500、5,000のデータを生成し、一次の自己回帰モデル ｙｔ=βｙt+εｔ （ただし、e1～N(0,1),ｙ0＝0）で、β=0.999, β=1.0, β=1.001のケースをそれぞれ推計する。これをそれぞれ10,000回繰り返し、各回において、βが真の値に等しいという帰無仮説につきt検定を行い、5％水準で棄却率を計算した。結果は表6のとおりである。
表6：帰無仮説の棄却率
表6をみると、β=0.999, β=1.0では、サンプル数が500から5,000に増えると棄却率は減少するが、β=1.001（非定常）のケースでは、棄却率が増加している。この結果は、非定常の時系列データでは、帰無仮説の棄却率が過大であり、検定結果の解釈につき、注意が必要であることを示唆している。
VII.結論
Hallのランダムウォーク仮説を最新のデータによって検証すると、消費の2期以上のラグ、所得と株価指数のラグが現在の消費に対して説明力をもたないことが分かった。モンテカルロ法とRWRによって、これらの結果が頑健であることも分かった。ICSラグはすべてのデータ期間を対象とすると、ランダムウォーク仮説を棄却したが、RWRでは、説明力をもたなかった。非定常な時系列データの回帰では、検定結果の解釈に注意が必要であることも分かった。
総じて、本稿は、純粋な意味でのランダムウォーク仮説を棄却する。しかし、ICSが恒常 所得の変化についての情報を現在の消費よりも素早く反映させているのであれば、修正仮説を支持することになろう。本稿の結論は、Hall（1978）の論文における結論に近いものである。
参考文献
- Campbell, J.Y. and Mankiw, N.G. (1990), "Permanent Income, Current Income, and Consumption", Journal of Business & Economic Statistics, Vol.8, No.3, 265-279.
- Fama, E, F. (1975), "Short-Term Interest Rates as Predictors of Inflation", American Economic Review, Vol.65, No.3, 269-486.
- Hall, R.E. (1978), "Stochastic Implications of the Life Cycle-Permanent Income Hypothesis: Theory and Evidence", Journal of Political Economy, Vol.86, No.6, 971-987.
- Patterson, K.D. (1992), "The Service Flow Consumption Goods with an Application to Friedman's Permanent Income Hypothesis", Oxford Economic Papers, 44, 289-305.
- Romer, D. (2006), Advanced Macroeconomics. New York: McGraw-Hill